Find the position of point (4, 1) after it undergoes the transformations successively : Reflection about the line y=x−1
To find the position of the point (4, 1) after it undergoes the transformation of reflection about the line y=x−1, we will follow these steps:
Step 1: Identify the line of reflection
The line of reflection is given by the equation y=x−1. We can rewrite this in standard form:
x−y−1=0
Step 2: Find the slope of the line
The slope of the line y=x−1 is 1. The slope of a line perpendicular to this line (which will be used to find the reflection) will be the negative reciprocal:
slope=−1
Step 3: Write the equation of the perpendicular line
Using the point (4, 1) and the slope -1, we can write the equation of the line perpendicular to y=x−1:
y−1=−1(x−4)
Simplifying this:
y−1=−x+4⟹y=−x+5
Step 4: Find the intersection point of the two lines
Now we need to find the intersection of the two lines y=x−1 and y=−x+5. Setting them equal to each other:
x−1=−x+5
Solving for x:
2x=6⟹x=3
Now substituting x=3 back into one of the equations to find y:
y=3−1=2
Thus, the intersection point is (3,2).
Step 5: Find the reflection point
The intersection point (3,2) is the midpoint between the original point (4,1) and its reflection (x′,y′). We can use the midpoint formula:
(4+x′2,1+y′2)=(3,2)
From this, we can set up the equations:
1. 4+x′2=3
2. 1+y′2=2
Solving the first equation:
4+x′=6⟹x′=2
Solving the second equation:
1+y′=4⟹y′=3
Final Result
The reflection of the point (4,1) about the line y=x−1 is (2,3).
The line of reflection is given by the equation y=x−1. We can rewrite this in standard form:
x−y−1=0
The slope of the line y=x−1 is 1. The slope of a line perpendicular to this line (which will be used to find the reflection) will be the negative reciprocal:
slope=−1
Using the point (4, 1) and the slope -1, we can write the equation of the line perpendicular to y=x−1:
y−1=−1(x−4)
Simplifying this:
y−1=−x+4⟹y=−x+5
Now we need to find the intersection of the two lines y=x−1 and y=−x+5. Setting them equal to each other:
x−1=−x+5
Solving for x:
2x=6⟹x=3
Now substituting x=3 back into one of the equations to find y:
y=3−1=2
Thus, the intersection point is (3,2).
The intersection point (3,2) is the midpoint between the original point (4,1) and its reflection (x′,y′). We can use the midpoint formula:
(4+x′2,1+y′2)=(3,2)
From this, we can set up the equations:
1. 4+x′2=3
2. 1+y′2=2
4+x′=6⟹x′=2
Solving the second equation:
1+y′=4⟹y′=3
The reflection of the point (4,1) about the line y=x−1 is (2,3).
Similar Questions
Find the position of point (4, 1) after it undergoes the transformations successively : Translation by one unit along x-axis in the positive direction.
View SolutionThe point (4, 1) undergoes the following three transformations successively: (a) Reflection about the line y = x (b) Translation through a distance 2 units along the positive direction of the x-axis. (c) Rotation through an angle π4 about the origin in the anti clockwise direction. The final position of the point is given by the co-ordinates.
View Solution
Knowledge Check
The point (4,1) undergoes the following two successive transformations
(i) Reflection about the line y=x
(ii) Translation through a distance of 2 units along the positive x-axis.
The coordinates of the new point areA(4,3)B(3,4)C(1,4)D(73,72)
The point (4, 1) undergoes the following three transformations successively: (a) Reflection about the line y = x (b) Translation through a distance 2 units along the positive direction of the x-axis. (c) Rotation through an angle π4 about the origin in the anti clockwise direction. The final position of the point is given by the co-ordinates.
View SolutionThe point (4,1) undergoes the following two successive transformations
(i) Reflection about the line y=x
(ii) Translation through a distance 2 units along the positive X-axis.
Then the final coordinate of the point are
View SolutionThe point (4,1) undergoes the following three successive transformations ,
reflection about the line y=x−1
translation through a distance 1 unit along the positive direction
rotation thrpough an angle π4 about the origin in the anti - clockwise direction
Then the coordinates of the final point are ,
View SolutionFind the reflection of the point P(-1,3) in the line x = 2
View SolutionFind the position of the points (1,1)and(2,−1) with respect to the line 3x+4y−6=0.
View SolutionFind the reflection of the point Q(2,1) in the line y + 3 = 0
View SolutionFind the position of the final image after three successive reflections taking the first reflection on m1 .
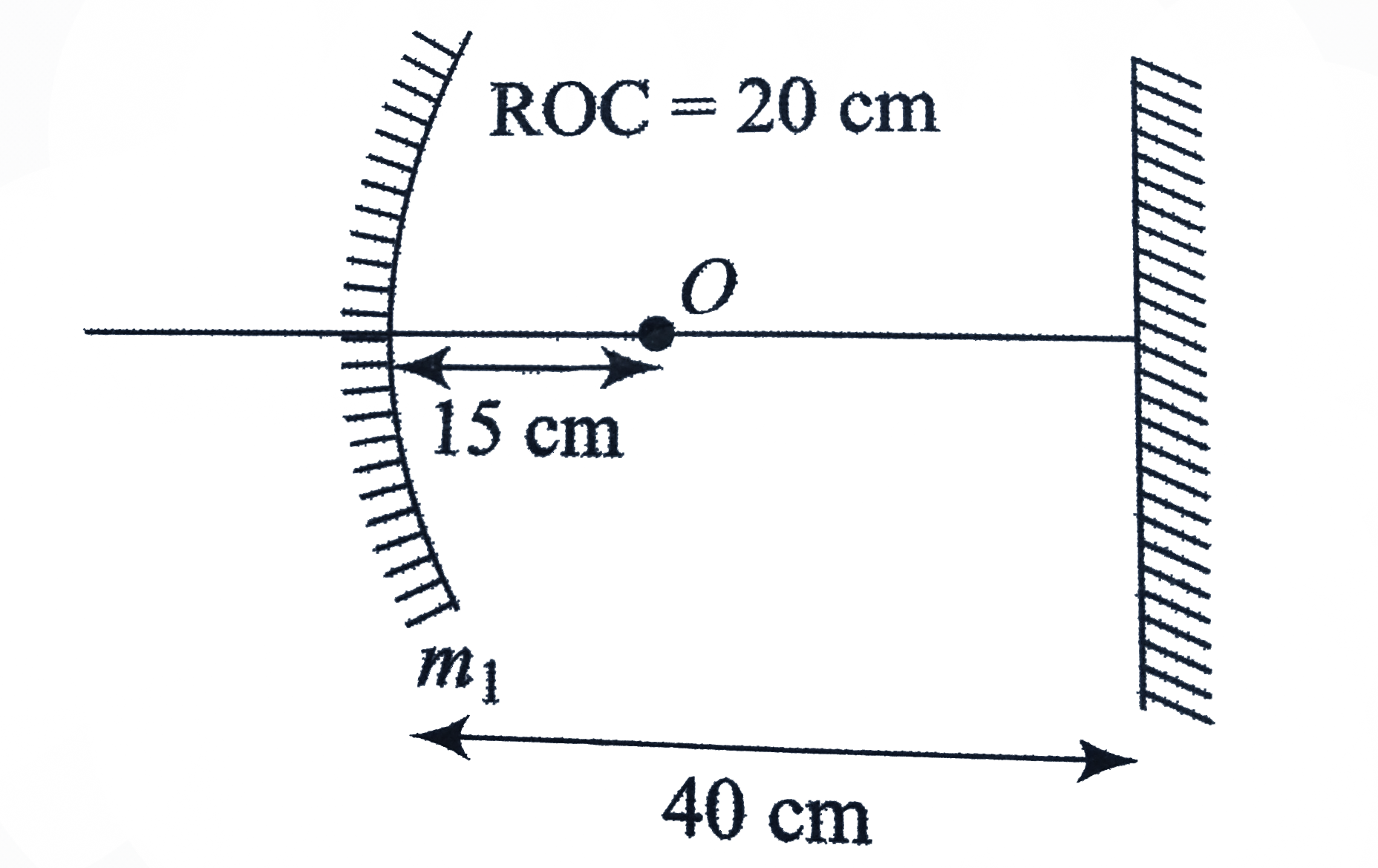
View Solution
