Show that the coordinates of the orthocentre of ΔABC is : (x1asecA+x2bsecB+x3csecCasecA+bsecB+csecA),y1asecA+y2bsecB+y3csecCasecA+bsecB+csecC)
Step by step video & image solution for Show that the coordinates of the orthocentre of DeltaABC is : ((x_1 a sec A + x_2 b sec B + x_3 c sec C)/(a sec A + b sec B + c sec A)), (y_1 a sec A + y_2 b sec B + y_3 c sec C)/(a sec A + b sec B + c sec C)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Prove the following identities :
secAsecA+1+secAsecA−1=2cosec2A
View SolutionIfcosecA+secA=cosecB+secB, prove that tanAtanB=cot(A+B)2
View Solutionsec4A−sec2A is equal to
View Solutionsec72∘−sec36∘=2.
View SolutionProve the following identities :
cot2A(secA−11+sinA)+sec2A(sinA−11+secA)=0
View SolutionIn ΔABC,∠B=90∘
Evaluate : cosec A cos C - sin A sec C .
View Solutionsec2A+sec2(π2−A)=sec2Asec2(π2−A)
View SolutionFigure given here shows the variation of velocity of a particle with time.
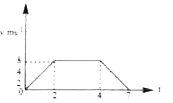
Find the following:
(i) Displacement during the time intervals.
(a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec
(ii) Accelerations at
(a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec.
(iii) Average acceleration
(a) between t = 0 to t = 4 sec.
(b) between t = 0 to t = 7 sec.
(iv) Average velocity during the motion.
View SolutionProve that in an acute angled triangle ABC,secA+secB+secC≥6.
View SolutionThe value of ∫secx(2+secx)(1+2secx)2dx, is equal to
View Solution
