AB is a side of a regular hexagon ABCDEF and is of length a with A as the origin and AB and AE as the x-axis andy-axis respectively. Find the equation of lines AC,AF and BE
To find the equations of the lines AC, AF, and BE in a regular hexagon ABCDEF with A at the origin, AB along the x-axis, and AE along the y-axis, we can follow these steps:
Step 1: Determine the Coordinates of the Vertices
In a regular hexagon with side length a:
- A(0,0)
- B(a,0)
- C(a2,a√32)
- D(−a2,a√32)
- E(−a,0)
- F(−a2,−a√32)
Step 2: Find the Equation of Line AC
The slope m of line AC can be calculated using the coordinates of points A(0,0) and C(a2,a√32):
mAC=y2−y1x2−x1=a√32−0a2−0=a√3/2a/2=√3
Using the point-slope form of the line equation, y−y1=m(x−x1):
y−0=√3(x−0)⟹y=√3x
Step 3: Find the Equation of Line AF
For line AF, we use points A(0,0) and F(−a2,−a√32):
mAF=−a√32−0−a2−0=−a√32−a2=√3
Using the point-slope form:
y−0=−√3(x−0)⟹y=−√3x
Step 4: Find the Equation of Line BE
For line BE, we use points B(a,0) and E(−a,0). The slope m is:
mBE=0−0−a−a=0
Since it is a horizontal line, the equation is simply:
y=0
Final Equations
- The equation of line AC is y=√3x.
- The equation of line AF is y=−√3x.
- The equation of line BE is y=0.
In a regular hexagon with side length a:
- A(0,0)
- B(a,0)
- C(a2,a√32)
- D(−a2,a√32)
- E(−a,0)
- F(−a2,−a√32)
The slope m of line AC can be calculated using the coordinates of points A(0,0) and C(a2,a√32):
mAC=y2−y1x2−x1=a√32−0a2−0=a√3/2a/2=√3
Using the point-slope form of the line equation, y−y1=m(x−x1):
y−0=√3(x−0)⟹y=√3x
For line AF, we use points A(0,0) and F(−a2,−a√32):
mAF=−a√32−0−a2−0=−a√32−a2=√3
Using the point-slope form:
y−0=−√3(x−0)⟹y=−√3x
For line BE, we use points B(a,0) and E(−a,0). The slope m is:
mBE=0−0−a−a=0
Since it is a horizontal line, the equation is simply:
y=0
- The equation of line AC is y=√3x.
- The equation of line AF is y=−√3x.
- The equation of line BE is y=0.
Similar Questions
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

equation of line AB.
View SolutionIn the given figure ABC is a triangle and BC is parallel to the Y-axis. AB and AC intersects the y-axis at Pand Q respectively.
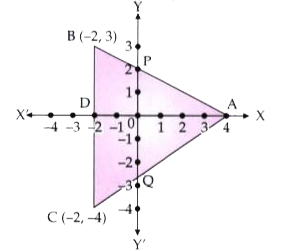
(iv) Find the equation of the line AC.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

co-ordinates of A and B.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
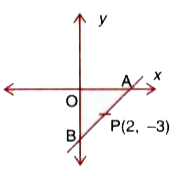
slope of line AB
View SolutionIn a regular hexagon ABCDEF, AB||ED|| x-axis. What are the slopes of its sides?
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
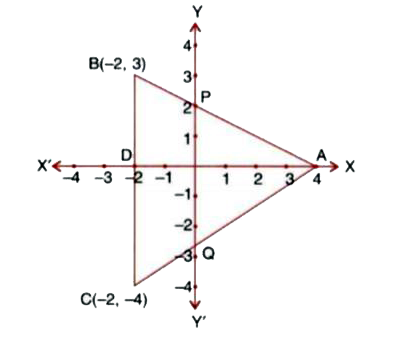
Find the length of AB and AC.
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.
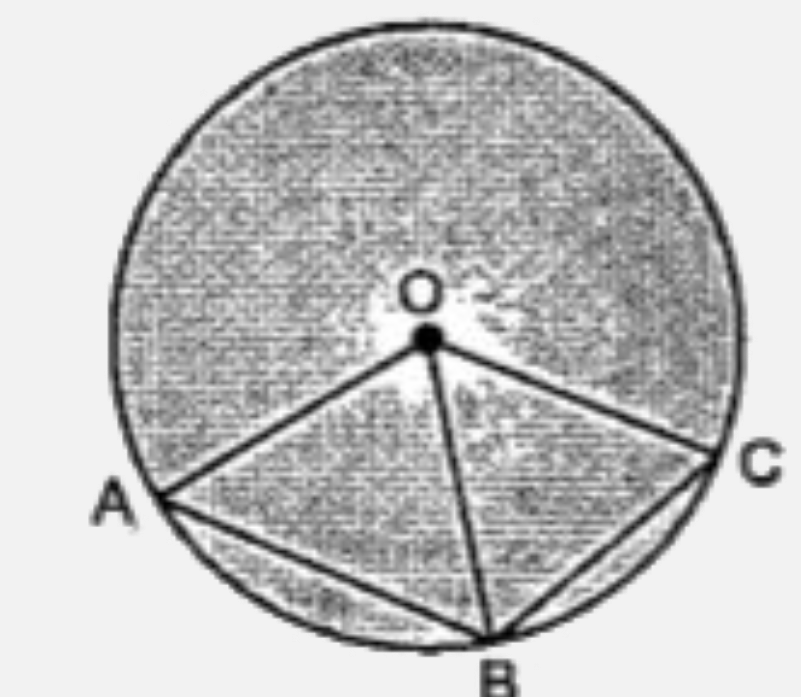
∠AOC
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.

∠OBA
View SolutionIn the given AB is a side of regular pentagon and BC is a side of regular hexagon.

∠AOB
View Solution
