ABC is a right angled triangle, right-angled at A. The coordinates of BandC are (6, 4) and ((14, 10) respectively. The angle between the side AB and x-axis is 450. Find the coordinates of A.
To solve the problem, we need to find the coordinates of point A in the right-angled triangle ABC, where the right angle is at A, and the coordinates of points B and C are given as (6, 4) and (14, 10) respectively. The angle between side AB and the x-axis is 45 degrees.
1. Understanding the Triangle:
- We know that triangle ABC is right-angled at A. Therefore, the slopes of lines AB and AC will be negative reciprocals of each other.
2. Finding the Slope of AB:
- Since the angle between AB and the x-axis is 45 degrees, the slope of line AB can be either mAB=1 (if it is a positive slope) or mAB=−1 (if it is a negative slope).
3. Case 1: Slope of AB is 1:
- The equation of line AB can be written as:
y=x+c
- Substituting the coordinates of point B (6, 4) into the equation:
4=6+c⟹c=4−6=−2
- Therefore, the equation of line AB is:
y=x−2
- The coordinates of point A can be expressed as:
A=(x,x−2)
4. Finding the Slope of AC:
- Since AB and AC are perpendicular, the slope of AC will be:
mAC=−1
- Using the coordinates of point C (14, 10), we can write the slope equation:
(x−2)−10x−14=−1
- Simplifying this gives:
x−12=−x+14⟹2x=26⟹x=13
- Thus, the coordinates of point A in this case are:
A=(13,13−2)=(13,11)
5. Case 2: Slope of AB is -1:
- The equation of line AB can be written as:
y=−x+c
- Substituting the coordinates of point B (6, 4):
4=−6+c⟹c=10
- Therefore, the equation of line AB is:
y=−x+10
- The coordinates of point A can be expressed as:
A=(x,10−x)
6. Finding the Slope of AC:
- Since the slope of AB is -1, the slope of AC will be:
mAC=1
- Using the coordinates of point C (14, 10):
(10−x)−10x−14=1
- Simplifying this gives:
−x=x−14⟹2x=14⟹x=7
- Thus, the coordinates of point A in this case are:
A=(7,10−7)=(7,3)
Conclusion:
The coordinates of point A can be either (13, 11) or (7, 3).
- We know that triangle ABC is right-angled at A. Therefore, the slopes of lines AB and AC will be negative reciprocals of each other.
- Since the angle between AB and the x-axis is 45 degrees, the slope of line AB can be either mAB=1 (if it is a positive slope) or mAB=−1 (if it is a negative slope).
- The equation of line AB can be written as:
y=x+c
- Substituting the coordinates of point B (6, 4) into the equation:
4=6+c⟹c=4−6=−2
- Therefore, the equation of line AB is:
y=x−2
- The coordinates of point A can be expressed as:
A=(x,x−2)
- Since AB and AC are perpendicular, the slope of AC will be:
mAC=−1
- Using the coordinates of point C (14, 10), we can write the slope equation:
(x−2)−10x−14=−1
- Simplifying this gives:
x−12=−x+14⟹2x=26⟹x=13
- Thus, the coordinates of point A in this case are:
A=(13,13−2)=(13,11)
- The equation of line AB can be written as:
y=−x+c
- Substituting the coordinates of point B (6, 4):
4=−6+c⟹c=10
- Therefore, the equation of line AB is:
y=−x+10
- The coordinates of point A can be expressed as:
A=(x,10−x)
- Since the slope of AB is -1, the slope of AC will be:
mAC=1
- Using the coordinates of point C (14, 10):
(10−x)−10x−14=1
- Simplifying this gives:
−x=x−14⟹2x=14⟹x=7
- Thus, the coordinates of point A in this case are:
A=(7,10−7)=(7,3)
The coordinates of point A can be either (13, 11) or (7, 3).
Similar Questions
Knowledge Check
- Question 1 - Select One
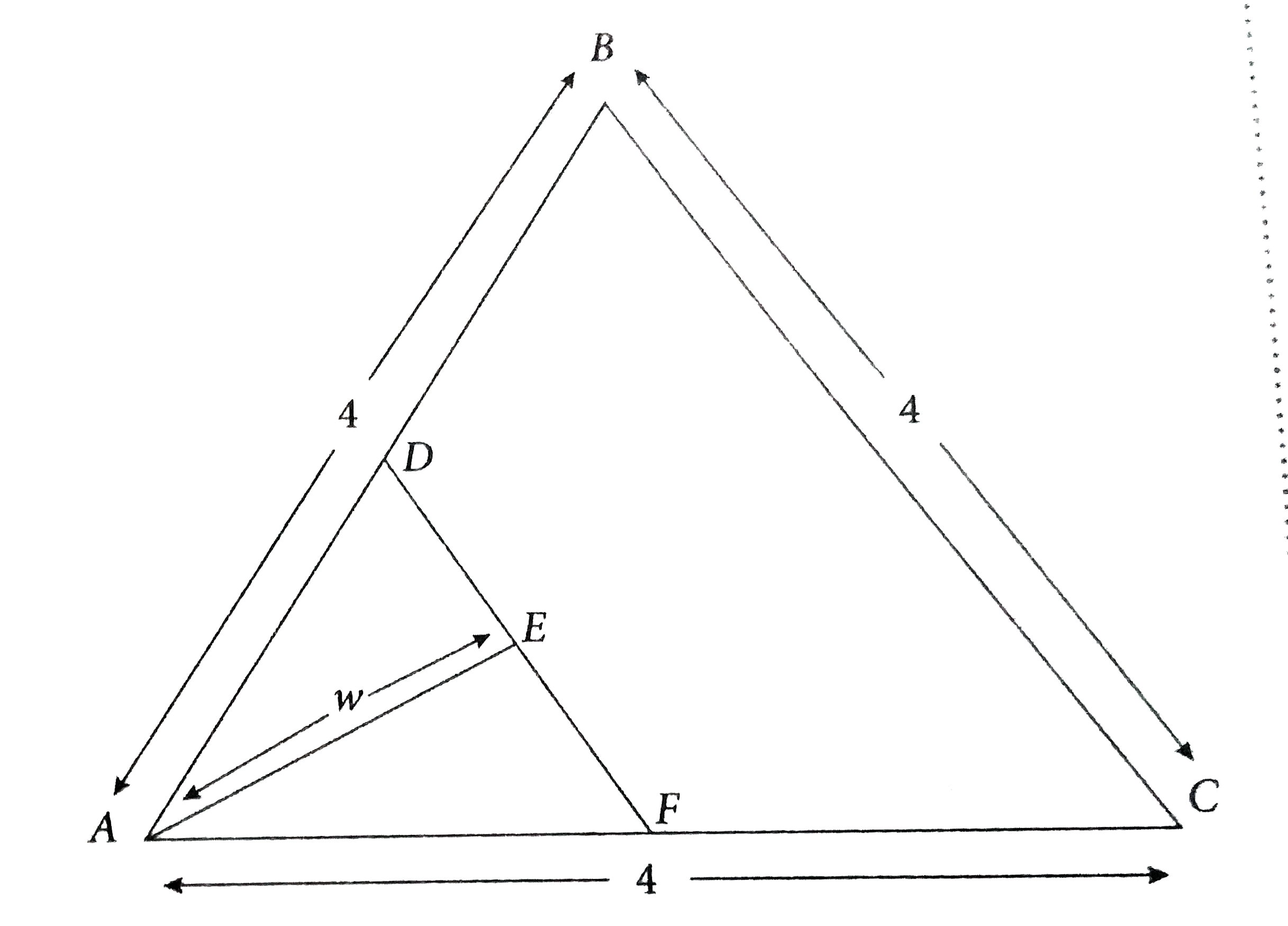
ΔABC is equilateral and ∠AEF is a right angle . D and F are the midpoints of AB and AC, respectively. What is the value of w?A1B√3C2D2√3
The distance of incentre of the right-angled triangle ABC (right angled at A) from B and C are √10and√5, respectively. The perimeter of the triangle is _____
View SolutionIf the sides of a right angled triangle are in A.P then the sines of the acute angles are
View SolutionThe coordinates of the points A, B, C are (0, 4), (2, 5) and (3 , 3) respectively. Prove that AB=BC and the angle ABC is a right angle.
View SolutionABC is a triangle right angled at C. If AB=25cmandAC=7cm, find BC.
View SolutionIn a right triangle ABC, right angled at C, if a = 7 cm and b = 7√3 cm, then ∠A=
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
 View Solution
View SolutionConstruct a right triangle, right angled at C in which AB=5.2\ cm and BC=4.6 cm.
View Solution

