The normals at P,Q and R are concurrent and PQ meets the diameter through R on the directrix x=-a . Prove that PQ touches [or PQ enveleopes] the parabola y2+16a(x+a)=0.
Step by step video & image solution for The normals at P,Q and R are concurrent and PQ meets the diameter through R on the directrix x=-a . Prove that PQ touches [or PQ enveleopes] the parabola y^2+16a(x+a)=0. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The normals at P, Q, R on the parabola y2=4ax meet in a point on the line y=c. Prove that the sides of the triangle PQR touch the parabola x2=2cy.
View SolutionPQ is a double ordinate of the ellipse x2+9y2=9, the normal at P meets the diameter through Q at R .then the locus of the mid point of PR is
View SolutionThe normal at P(8, 8) to the parabola y2=8x cuts it again at Q then PQ =
View SolutionThe normals at the extremities of a chord PQ of the parabola y2=4ax meet on the parabola, then locus of the middle point of PQ is
View SolutionPQ is a double ordinate of the parabola y2=4ax. If the normal at P intersect the line passing through Q and parallel to axis of x at G, then locus of G is a parabola with -
View SolutionThe straight line 2x+3y=24 meets the x-axis at P and the y-axis at Q. The perpendicular bisector of PQ meets the line through (-2,0) parallel to the y-axis at R. Find the area of the ΔPQR.
View SolutionThe normal to the parabola y2=4x at P (1, 2) meets the parabola again in Q, then coordinates of Q are
View SolutionThe normal to the parabola y2=4x at P(9,6) meets the parabola again at Q. If the tangent at Q meets the directrix at R, then the slope of another tangent drawn from point R to this parabola is
View SolutionIf a chord PQ of the parabola y2=4ax subtends a right angle at the vertex, show that the locus of the point of intersection of the normals at P and Q is y2=16a(x−6a).
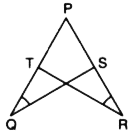
View SolutionThe given figure shows PQ=PRand∠Q=∠R.
Prove that ΔPQS=ΔPRT
View Solution
