Data could not be retrieved.
To solve the problem involving two complex numbers z1 and z2 given the condition |z1+z2|2=|z1|2+|z2|2, we can follow these steps:
Step 1: Expand the left-hand side
We start with the left-hand side of the equation:
|z1+z2|2=(z1+z2)(¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯z1+z2)=(z1+z2)(¯¯¯¯¯z1+¯¯¯¯¯z2)
Expanding this gives:
|z1+z2|2=z1¯¯¯¯¯z1+z1¯¯¯¯¯z2+z2¯¯¯¯¯z1+z2¯¯¯¯¯z2=|z1|2+|z2|2+z1¯¯¯¯¯z2+z2¯¯¯¯¯z1
Step 2: Set up the equation
According to the problem, we have:
|z1+z2|2=|z1|2+|z2|2
Substituting the expanded form from Step 1, we get:
|z1|2+|z2|2+z1¯¯¯¯¯z2+z2¯¯¯¯¯z1=|z1|2+|z2|2
Step 3: Simplify the equation
By subtracting |z1|2+|z2|2 from both sides, we have:
z1¯¯¯¯¯z2+z2¯¯¯¯¯z1=0
Step 4: Express in terms of real parts
The expression z1¯¯¯¯¯z2+z2¯¯¯¯¯z1 can be rewritten as:
2Re(z1¯¯¯¯¯z2)=0
This implies:
Re(z1¯¯¯¯¯z2)=0
Step 5: Conclude the result
The condition Re(z1¯¯¯¯¯z2)=0 means that the complex number z1¯¯¯¯¯z2 is purely imaginary. This leads us to conclude that:
Re(z1z2)=0
Thus, the correct answer is:
Re(z1z2)=0
Final Answer
The correct option is:
Re(z1z2)=0
We start with the left-hand side of the equation:
|z1+z2|2=(z1+z2)(¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯z1+z2)=(z1+z2)(¯¯¯¯¯z1+¯¯¯¯¯z2)
Expanding this gives:
|z1+z2|2=z1¯¯¯¯¯z1+z1¯¯¯¯¯z2+z2¯¯¯¯¯z1+z2¯¯¯¯¯z2=|z1|2+|z2|2+z1¯¯¯¯¯z2+z2¯¯¯¯¯z1
According to the problem, we have:
|z1+z2|2=|z1|2+|z2|2
Substituting the expanded form from Step 1, we get:
|z1|2+|z2|2+z1¯¯¯¯¯z2+z2¯¯¯¯¯z1=|z1|2+|z2|2
By subtracting |z1|2+|z2|2 from both sides, we have:
z1¯¯¯¯¯z2+z2¯¯¯¯¯z1=0
The expression z1¯¯¯¯¯z2+z2¯¯¯¯¯z1 can be rewritten as:
2Re(z1¯¯¯¯¯z2)=0
This implies:
Re(z1¯¯¯¯¯z2)=0
The condition Re(z1¯¯¯¯¯z2)=0 means that the complex number z1¯¯¯¯¯z2 is purely imaginary. This leads us to conclude that:
Re(z1z2)=0
Thus, the correct answer is:
Re(z1z2)=0
The correct option is:
Re(z1z2)=0
Similar Questions
Study the climatic data given below and answer the questions that follow:

Why could it be correct to presume that the station lies in the interior and not on the coast ?
View SolutionA: The process of demodulation is carried out to retrieve the message signal.
R: The range of the line-of -sight propagatin is limited mainly due to earth's curvature.
View Solution
Knowledge Check
Secondary amines could be prepared by
Areduction of nitro compoundsBreduction of amidesCreduction of isonitrilesDreduction of isonitrilesIf |A|>19, which of the following could not be equal to A?
A26B22C18D−20After helping the woman to the Gujar encampment, Sibia returned to retrieve the ________
AgrassBsickleCforkDAll of these
What could be entry route of the allergens ?
View SolutionWhat could be the product for following reaction?

View SolutionWhat could be the product for the following reaction ?

View SolutionWhat could be the product for the following reaction ?
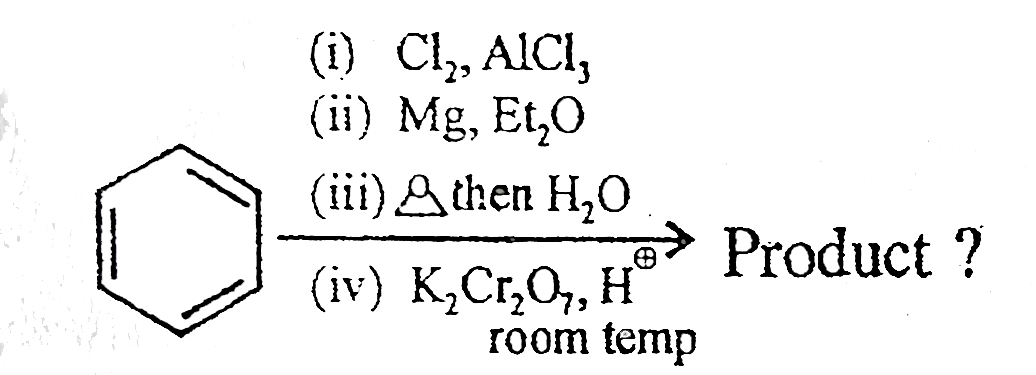
View SolutionThe virologist .... Showed that the viruses could be crystallized .
View Solution
