In an isosceles right angled triangle , a straight line drwan from the mid - point of one of equal sides to the opposite angle . It divides the angle into two parts , θand(π/4−θ) . Then tanθandtan[(π/4)−θ] are equal to
To solve the problem step by step, we will analyze the isosceles right-angled triangle and apply trigonometric identities.
1. Understanding the Triangle:
- Let triangle ABC be an isosceles right triangle with AB=AC and ∠A=π4.
- Let B and C be the equal sides, and G be the midpoint of side BC.
2. Labeling the Sides:
- Assume AB=AC=2x. Therefore, BG=GC=x.
3. Identifying Angles:
- The line AG divides ∠A into two parts: θ and π4−θ.
4. Using Triangle Properties:
- In triangle ABG, we can use the definition of tangent:
tan(θ)=oppositeadjacent=BGAB=x2x=12
- Therefore, we have:
tan(θ)=12
5. Finding tan(π4−θ):
- We use the tangent subtraction formula:
tan(π4−θ)=tan(π4)−tan(θ)1+tan(π4)tan(θ)
- Since tan(π4)=1, substituting the values gives:
tan(π4−θ)=1−121+1⋅12=121+12=1232=13
6. Conclusion:
- We have found that:
tan(θ)=12andtan(π4−θ)=13
Final Answer:
tan(θ)=12,tan(π4−θ)=13
- Let triangle ABC be an isosceles right triangle with AB=AC and ∠A=π4.
- Let B and C be the equal sides, and G be the midpoint of side BC.
- Assume AB=AC=2x. Therefore, BG=GC=x.
- The line AG divides ∠A into two parts: θ and π4−θ.
- In triangle ABG, we can use the definition of tangent:
tan(θ)=oppositeadjacent=BGAB=x2x=12
- Therefore, we have:
tan(θ)=12
- We use the tangent subtraction formula:
tan(π4−θ)=tan(π4)−tan(θ)1+tan(π4)tan(θ)
- Since tan(π4)=1, substituting the values gives:
tan(π4−θ)=1−121+1⋅12=121+12=1232=13
- We have found that:
tan(θ)=12andtan(π4−θ)=13
tan(θ)=12,tan(π4−θ)=13
Similar Questions
tan(π4+θ)−tan(π4−θ)=2tan2θ
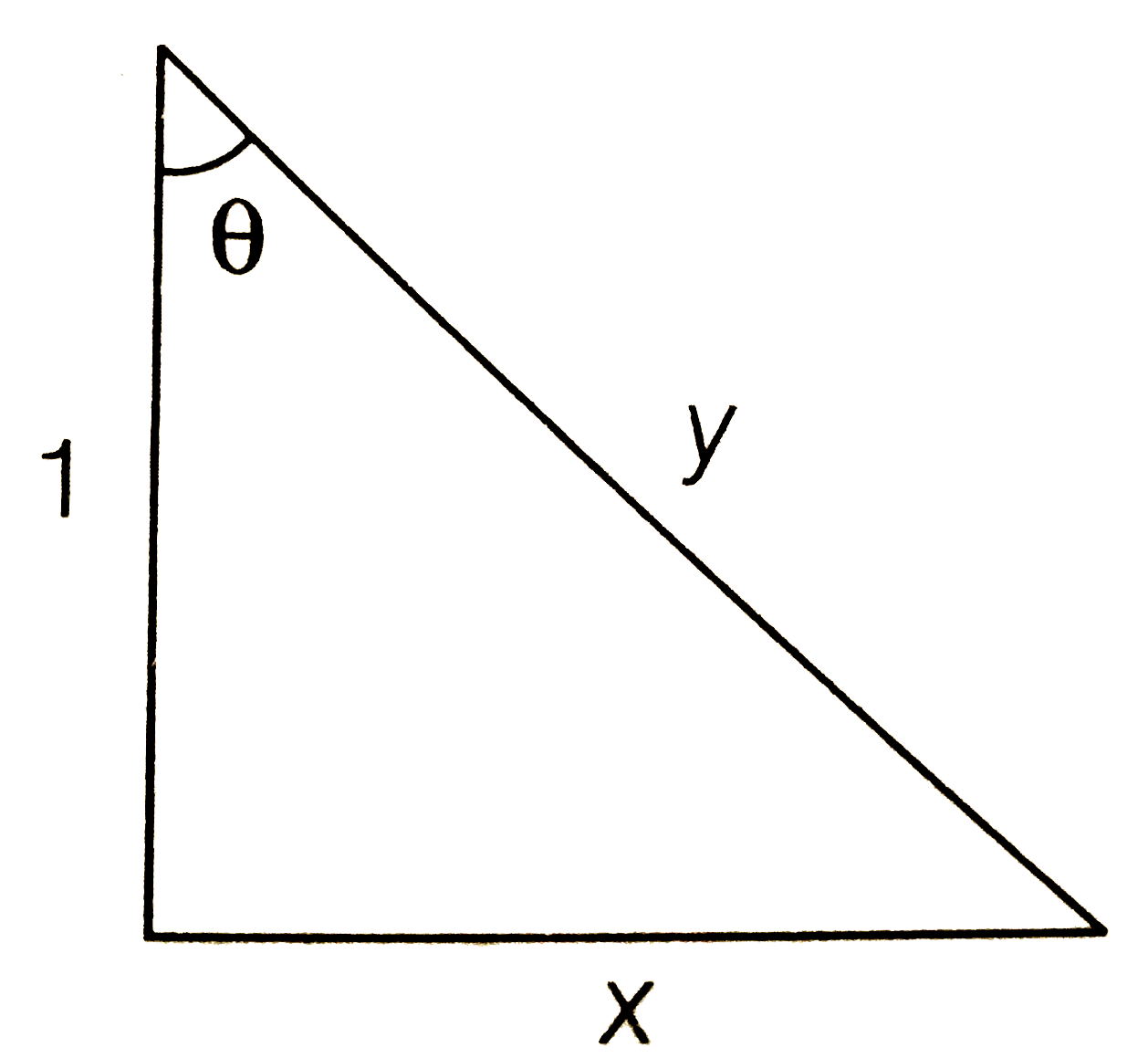
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as

View SolutionSolve tanθtan4θ=1 for 0<θ<π.
View SolutionProve that secθ+tanθ=tan(π4+θ2)
View SolutionIf tan(πcosθ)=cot(πsinθ) then sin(θ+π4) equals
View SolutionSolve :tan(π4+θ)+tan(π4−θ)=4
View SolutionIf π<θ<3π2 and cosθ=−35, then tan(θ4) is equal to
View SolutionIf tan(π2sinθ)=cot(π2cosθ), then sinθ+cosθ is equal to
View SolutionThe range of the function f(θ)=sinθθ+θtanθ,θ∈(0,π2) is equal to :
View SolutionIf θ is an acute angle and tanθ+secθ=1.5, find sinθ,tanθ and secθ.
View Solution
