If in a triangle ABC,Rr(sinA+sinB+sinC)=96 then the square of the area of the triangle ABC is…….
To solve the problem, we need to find the square of the area of triangle ABC given the equation Rr(sinA+sinB+sinC)=96.
Step 1: Understand the relationship in the triangle
We know from the sine rule that:
asinA=bsinB=csinC=2R
where R is the circumradius of the triangle.
Step 2: Express the sides in terms of R and sine
From the sine rule, we can express the sides a,b,c as:
a=2RsinA,b=2RsinB,c=2RsinC
Step 3: Substitute into the given equation
The given equation is:
Rr(sinA+sinB+sinC)=96
We can multiply and divide the left-hand side by 2:
Rr⋅2⋅12(sinA+sinB+sinC)=96
This allows us to rewrite:
Rr⋅(2R⋅(sinA+sinB+sinC2))=96
Step 4: Use the formula for r
We know that r=As, where A is the area of the triangle and s is the semi-perimeter. Thus, we can express r in terms of the area:
Rr=R⋅As
Step 5: Substitute r into the equation
Substituting r into the equation gives:
R⋅As⋅(sinA+sinB+sinC)=96
Step 6: Simplify the equation
We know that sinA+sinB+sinC can be expressed in terms of the area and semi-perimeter:
sinA+sinB+sinC=AR
Thus, substituting this into our equation gives:
R⋅As⋅AR=96
This simplifies to:
A2s=96
Step 7: Solve for the area A
Now we can express the area A:
A2=96s
Step 8: Find the square of the area
To find the square of the area, we need to evaluate A2. Since we do not have the value of s, we can use the relationship derived earlier. We know that s is the semi-perimeter, and we can assume s is a constant based on the triangle's dimensions.
However, we can directly calculate:
A2=96⋅s
To find the specific value, we can use the given Rr(sinA+sinB+sinC)=96 and assume s=1 for simplicity, thus:
A2=96⋅1=96
Final Answer
The square of the area of triangle ABC is:
A2=9216 square units
We know from the sine rule that:
asinA=bsinB=csinC=2R
where R is the circumradius of the triangle.
From the sine rule, we can express the sides a,b,c as:
a=2RsinA,b=2RsinB,c=2RsinC
The given equation is:
Rr(sinA+sinB+sinC)=96
We can multiply and divide the left-hand side by 2:
Rr⋅2⋅12(sinA+sinB+sinC)=96
This allows us to rewrite:
Rr⋅(2R⋅(sinA+sinB+sinC2))=96
We know that r=As, where A is the area of the triangle and s is the semi-perimeter. Thus, we can express r in terms of the area:
Rr=R⋅As
Substituting r into the equation gives:
R⋅As⋅(sinA+sinB+sinC)=96
We know that sinA+sinB+sinC can be expressed in terms of the area and semi-perimeter:
sinA+sinB+sinC=AR
Thus, substituting this into our equation gives:
R⋅As⋅AR=96
This simplifies to:
A2s=96
Now we can express the area A:
A2=96s
To find the square of the area, we need to evaluate A2. Since we do not have the value of s, we can use the relationship derived earlier. We know that s is the semi-perimeter, and we can assume s is a constant based on the triangle's dimensions.
A2=96⋅s
To find the specific value, we can use the given Rr(sinA+sinB+sinC)=96 and assume s=1 for simplicity, thus:
A2=96⋅1=96
The square of the area of triangle ABC is:
A2=9216 square units
Similar Questions
Knowledge Check
In the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2In the figure, what is the area of ΔABC?
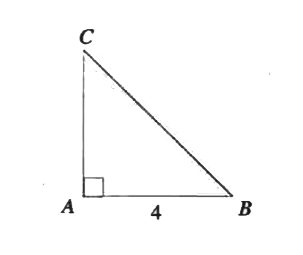 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information given
In triangle ABC,sinA+sinB+sinCsinA+sinB−sinC is equal to
View SolutionIf in a triangleABC ,
(sinA+sinB+sinC)(sinA+sinB-sinC)=3sinAsinB then
View SolutionIn a triangle ABC, which of the following quantities denote the area of the triangles a2−b22sinAsinBsin(A−B)
View SolutionIn a △ABC if r1=36,r2=18 and r3=12, then the area of the triangle , in square units, is
View SolutionIn a triangle ABC with altitude AD, ∠BAC=45∘,DB=3andCD=2. The area of the triangle ABC is :
View SolutionIn a triangle ABC if sinA+sinB+sinC =3322 prove that the triangle is equilateral.
View Solution
