The plane xa+yb+zc=1 meets the coordinate axes at A,B and C respectively. Find the equation of the sphere OABC.
To find the equation of the sphere OABC, where O is the origin and A, B, and C are the points where the plane xa+yb+zc=1 meets the coordinate axes, we can follow these steps:
Step 1: Identify the Points A, B, and C
The plane intersects the coordinate axes at:
- Point A on the x-axis: A(a,0,0)
- Point B on the y-axis: B(0,b,0)
- Point C on the z-axis: C(0,0,c)
Step 2: Write the General Equation of the Sphere
The general equation of a sphere in 3D space is given by:
x2+y2+z2+2gx+2fy+2hz+c=0
where g,f,h, and c are constants that we need to determine.
Step 3: Use the Points to Form Equations
Since the sphere passes through the points O, A, B, and C, we can substitute these points into the sphere's equation to form equations.
1. For Point O (0, 0, 0):
02+02+02+2g(0)+2f(0)+2h(0)+c=0⟹c=0
2. For Point A (a, 0, 0):
a2+02+02+2g(a)+2f(0)+2h(0)+c=0⟹a2+2ga=0
This simplifies to:
2ga=−a2⟹g=−a2
3. For Point B (0, b, 0):
02+b2+02+2g(0)+2f(b)+2h(0)+c=0⟹b2+2fb=0
This simplifies to:
2fb=−b2⟹f=−b2
4. For Point C (0, 0, c):
02+02+c2+2g(0)+2f(0)+2h(c)+c=0⟹c2+2hc=0
This simplifies to:
2hc=−c2⟹h=−c2
Step 4: Substitute the Values of g, f, h, and c into the Sphere Equation
Now we substitute g,f,h, and c back into the general equation of the sphere:
x2+y2+z2+2(−a2)x+2(−b2)y+2(−c2)z+0=0
This simplifies to:
x2+y2+z2−ax−by−cz=0
Final Equation of the Sphere
Thus, the equation of the sphere OABC is:
x2+y2+z2−ax−by−cz=0
The plane intersects the coordinate axes at:
- Point A on the x-axis: A(a,0,0)
- Point B on the y-axis: B(0,b,0)
- Point C on the z-axis: C(0,0,c)
The general equation of a sphere in 3D space is given by:
x2+y2+z2+2gx+2fy+2hz+c=0
where g,f,h, and c are constants that we need to determine.
Since the sphere passes through the points O, A, B, and C, we can substitute these points into the sphere's equation to form equations.
02+02+02+2g(0)+2f(0)+2h(0)+c=0⟹c=0
a2+02+02+2g(a)+2f(0)+2h(0)+c=0⟹a2+2ga=0
This simplifies to:
2ga=−a2⟹g=−a2
02+b2+02+2g(0)+2f(b)+2h(0)+c=0⟹b2+2fb=0
This simplifies to:
2fb=−b2⟹f=−b2
02+02+c2+2g(0)+2f(0)+2h(c)+c=0⟹c2+2hc=0
This simplifies to:
2hc=−c2⟹h=−c2
Now we substitute g,f,h, and c back into the general equation of the sphere:
x2+y2+z2+2(−a2)x+2(−b2)y+2(−c2)z+0=0
This simplifies to:
x2+y2+z2−ax−by−cz=0
Thus, the equation of the sphere OABC is:
x2+y2+z2−ax−by−cz=0
Similar Questions
The plane xa+yb+zc=1 meets the co-ordinate axes in the point A, B, C respectively. Find the
area △ABC.
View SolutionA tangent and a normal to a curve at any point P meet the x and y axes at A, B and C, D respectively. Find the equation of the curve passing through (1,0) if the centre of circle through O.C,PandB lies on the line y = x (where O is the origin).
View Solution
Knowledge Check
A plane meets the coordinate axes at A, B and C respectively such that the centroid of triangle ABC is (p, q, r). The equation of the plane is
Axp+yq+zr=1Bxp+yp+zr=13Cpz+qy+rz=3Dxp+yq+zr=3
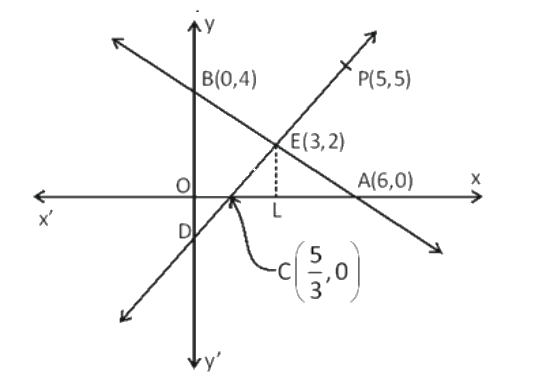
The line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionA plane meets the coordinate axes at A,BandC respectively such that the centroid of triangle ABC is (1,−2,3). Find the equation of the plane.
View SolutionA plane cuts the co-ordinate axes at A, B and C respectively. If the centroid of ΔABC is (2,−3,4), find the equation of the plane.
View SolutionIf the plane x2+y3+z6=1 cuts the axes of coordinates at points, A,B, and C, then find the area of the triangle ABC. a. 18 sq unit b. 36 sq unit c. 3√14 sq unit d. 2√14 sq unit
View SolutionThe plane x2+y3+z4=1 cuts the co-ordinate axes in A,B,C: then the area of the ΔABC is
View SolutionThe line xa+yb=1 meets the axis of and y at A and B respectively and C is middle point of AB then
View SolutionIf the plane x2+y3+z4=1 cuts the coordinate axes in A,B,C, then the area of triangle ABC is
View Solution
