X and Y are two sets and f:X→Y If {f(c)=y;c⊂X,y⊂Y} and {f−1(d)=x;d⊂Y,x⊂X, then the true statement is (a)f(f−1(b))=b (b)f−1(f(a))=a (c)f(f−1(b))=b,b⊂y (d)f−1(f(a))=a,a⊂xSolution in Tamil
Step by step video & image solution for X and Y are two sets and f: X->Y If {f(c)=y; c subX, y subY} and {f^(-1)(d)=x;d subY,x sub X, then the true statement is (a) f(f^(-1)(b))=b (b) f^(-1)(f(a))=a (c) f(f^(-1)(b))=b, b sub y (d) f^(-1)(f(a))=a, a sub x by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If f(x)=limn→∞n(x1n−1),thenforx>0,y>0,f(xy) is equal to : (a)f(x)f(y) (b) f(x)+f(y) (c)f(x)−f(y) (d) none of these
View SolutionGiven the graph of y=f(x).
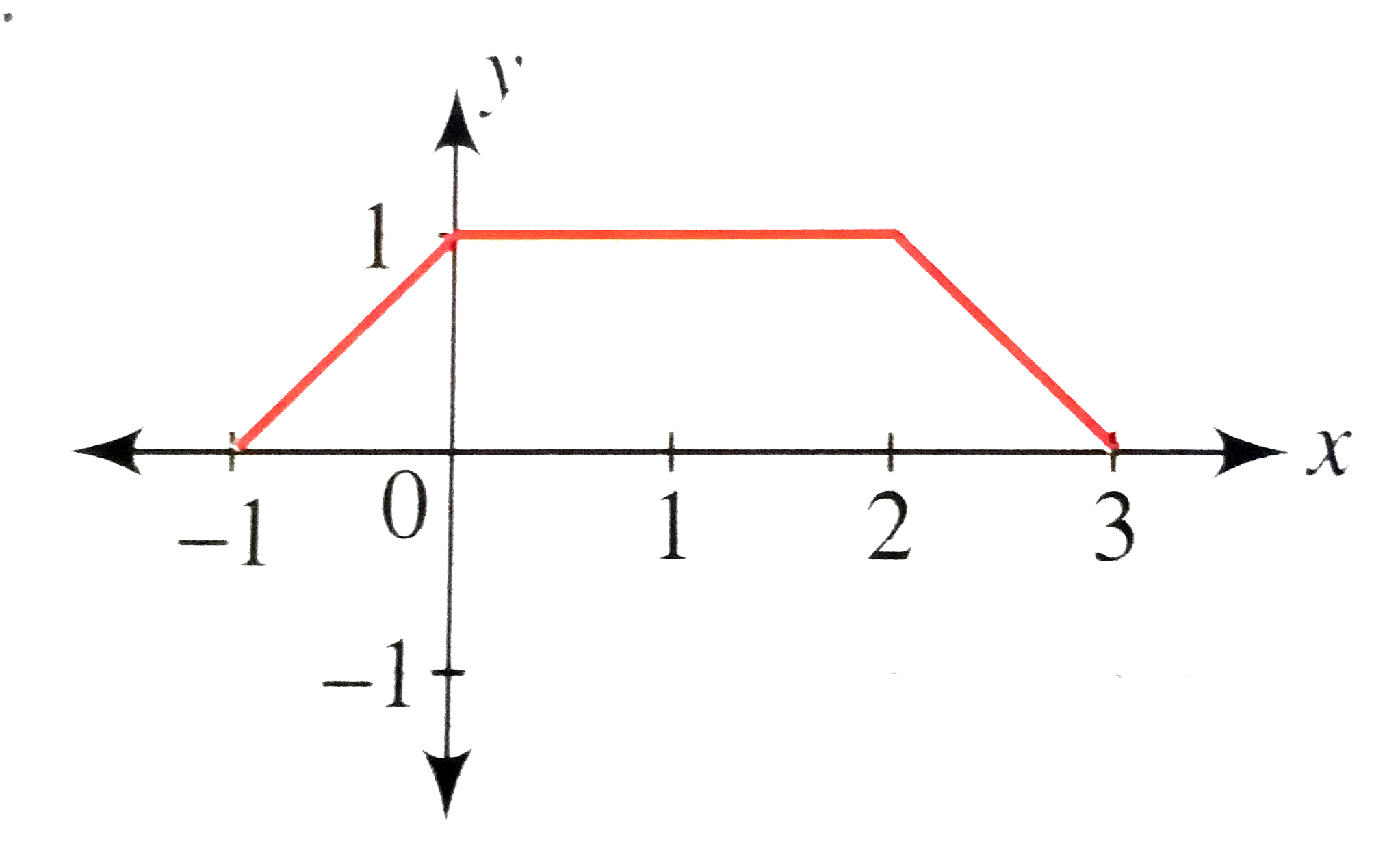
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)
View SolutionLet f(x)=|x−1|. Then (a)f(x2)=(f(x))2 (b) f(x+y)=f(x)+f(y) (c)f(|x|)=|f(x)| (d) none of these
View SolutionIf y = f(x) = ((x+2))/((x-1)) , then (a) x = f(y) (b) f(1) = 3 (c) y increases with x for x < 1 (d) f is a rational function of x
View SolutionIf X and Y are two non-empty sets where f: X->Y ,is function is defined such that f(c) = {f (x): x in C} for C sube X and f^-1 (D) = {x: f(x) in D} for D sube Y ,for any A sube Y and B sube Y , then
View SolutionLet f(x)=|x−1|. Then (a)f(x2)=(f(x))2 (b) f(x+y)=f(x)+f(y) (c)f(|x|)−|f(x)| (d) none of these
View SolutionX and Y are two sets and f:X→Y If {f(c)=y;c⊂X,y⊂Y} and {f−1(d)=x;d⊂Y,x⊂X, then the true statement is (a)f(f−1(b))=b (b)f−1(f(a))=a (c)f(f−1(b))=b,b⊂y (d)f−1(f(a))=a,a⊂x
View Solution
