Discuss the applicability of Rolles theorem for the following
functions on the indicated intervals:
f(x)=|x|∈[−1,1]
f(x)=3+(x−2)2/3
in [1,3]
f(x)=tanx∈[0,π]
f(x)=log{x2+abx(a+b)}
in [a,b], where 0 less than a less than bSolution in Tamil
Step by step video & image solution for Discuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=|x|in[-1,1] f(x)=3+(x-2)^(2//3) in [1,3] f(x)=tanx in [0,pi] f(x)=log{(x^2+a b)/(x(a+b))} in [a,b], where 0 less than a less than b by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Discuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=|x|∈[−1,1] f(x)=3+(x−2)2/3 in [1,3] f(x)=tanξn[0,π] f(x)=log{x2+abx(a+b)} in [a,b],where≺a<b
06:17View SolutionDiscuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=|x|∈[−1,1] f(x)=3+(x−2)2/3 in [1,3] f(x)=tanξn[0,π] f(x)=log{x2+abx(a+b)} in [a,b],where≺a<b
05:26View SolutionVerify Rolle theorem for the function f(x)=log{x2+abx(a+b)}on[a,b], where 0<a<b.
05:12View SolutionIn BX3 B - X distance is shorter than what is expected theoretically because (X = F, CI, Br, I)
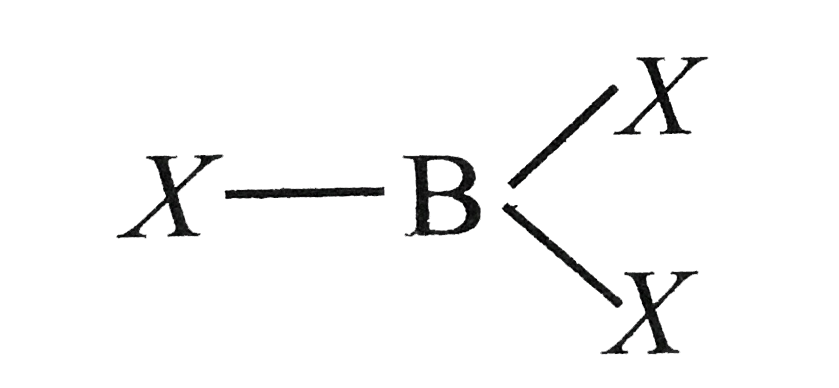 03:39View Solution
03:39View SolutionDiscuss the applicability of Rolles theorem for the following functions on the indicated intervals: f(x)=3+(x−2)2/3 in [1,3]
02:49View SolutionIf the function f(x)=ax3+bx2+11x−6 satisfies conditions of Rolles theorem in [1,3]andf'(2+1√3)=0, then values of aandb, respectively, are
06:35View SolutionDiscuss the applicability of Rolle's theorem to f(x) = log [(x^(2) + ab)/((a+b)x)] , in the interval [a,b].
04:11View Solution

