A continuous, even periodic function f with period 8 is such that f(0) =0.f(1)=2.f(2)=1f(3)=2.f(4)=3. then the value of cos−1(cos(f(9)+2f(20))) is equal to Solution in Tamil
Step by step video & image solution for A continuous, even periodic function f with period 8 is such that f(0) =0.f(1)=2.f(2)=1f(3)=2.f(4)=3. then the value of cos^-1(cos(f(9)+2f(20))) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A continuous, even periodic function f with period 8 is such that f(0)=0,f(1)=−2,f(2)=1,f(3)=2,f(4)=3, then the value of tan−1tan{f(−5)+f(20)+cos−1(f(−10))+f(17)} is equal to
View SolutionIf f is a function such that f(0) = 2, f(1) = 3, f(x+2) = 2f(x) - f(x + 1), then f(5) is
View SolutionGiven below is a partial graph of an even periodic function f whose period is 8. If [*] denotes greatest integer function then find the value of the expression.
f(−3)+2|f(−1)|+[f(78)]+f(0)+arccos(f(−2))+f(−7)+f(20)
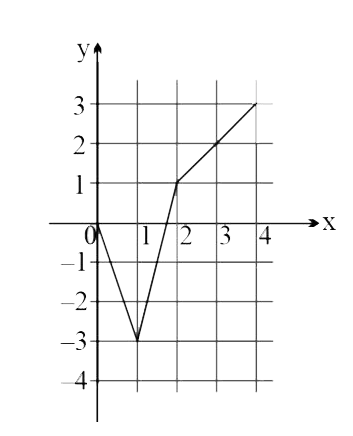
View SolutionIf a function F is such that F(0)=2 , F(1)=3 , F(n+2)=2F(n)-F(n+1) for n ge 0 , then F(5) is equal to
View SolutionA continuous, even periodic function f with period 8 is such that f(0) =0.f(1)=−2.f(2)=1f(3)=2.f(4)=3. then the value of cos−1(cos(f(9)+2f(20))) is equal to
View SolutionLet f:(−5,5)→R be a differentiable function of with f(4)=1,f'(4)=1,f(0)=−1andf'(0)=Ifg(x)=(f(2f2(x)+2))2, then g'(0) equals
View SolutionA continuous, even periodic function f with period 8 is such that f(0)=0,f(1)=−2,f(2)=1,f(3)=2,f(4)=3, then the value of tan−1tan{f(−5)+f(20)+cos−1(f(−10))+f(17)} is equal to
View Solution
