A bag contains 50 tickets numbered 1, 2, 3, .., 50 of which five are drawn at random and arranged in ascending order of magnitude (x1<x2<x3<x4<x5). Find the probability that x3=30.Solution in Tamil
The correct Answer is:.29C2×.20C2.50C5
Five tickets out of 50 can be drawn in .50C5 ways. Since x1<x2<x3<x4<x5 and x3=30, we have x1,x2<30, i.e., x1 and x2 should come from tickets numbered 1 and 29 and this may happen in .29C2. Remaining ways, i.e., x4,x5>30, should come from 20 tickets numbered 31 to 50 in .20C2 ways.
So, favorable number of cases is .29C2.20C2. Hence, required probability is
.29C2×.20C2.50C5
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.37videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Single)46videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise 9.16videos
PROBABILITY I
- BOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank24videos
PROBABILITY AND STATISTICS
- BOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - JEE Advanced Previous Year25videos
PROBABILITY II
Similar Questions
AandB are two candidates seeking admission in ITT. The probability that A is selected is 0.5 and the probability that AandB are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9?
01:05View SolutionA sample space consists of 3 sample points with associated probabilities given as 2p,p2,4p−1. Then the value of p is
04:27View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
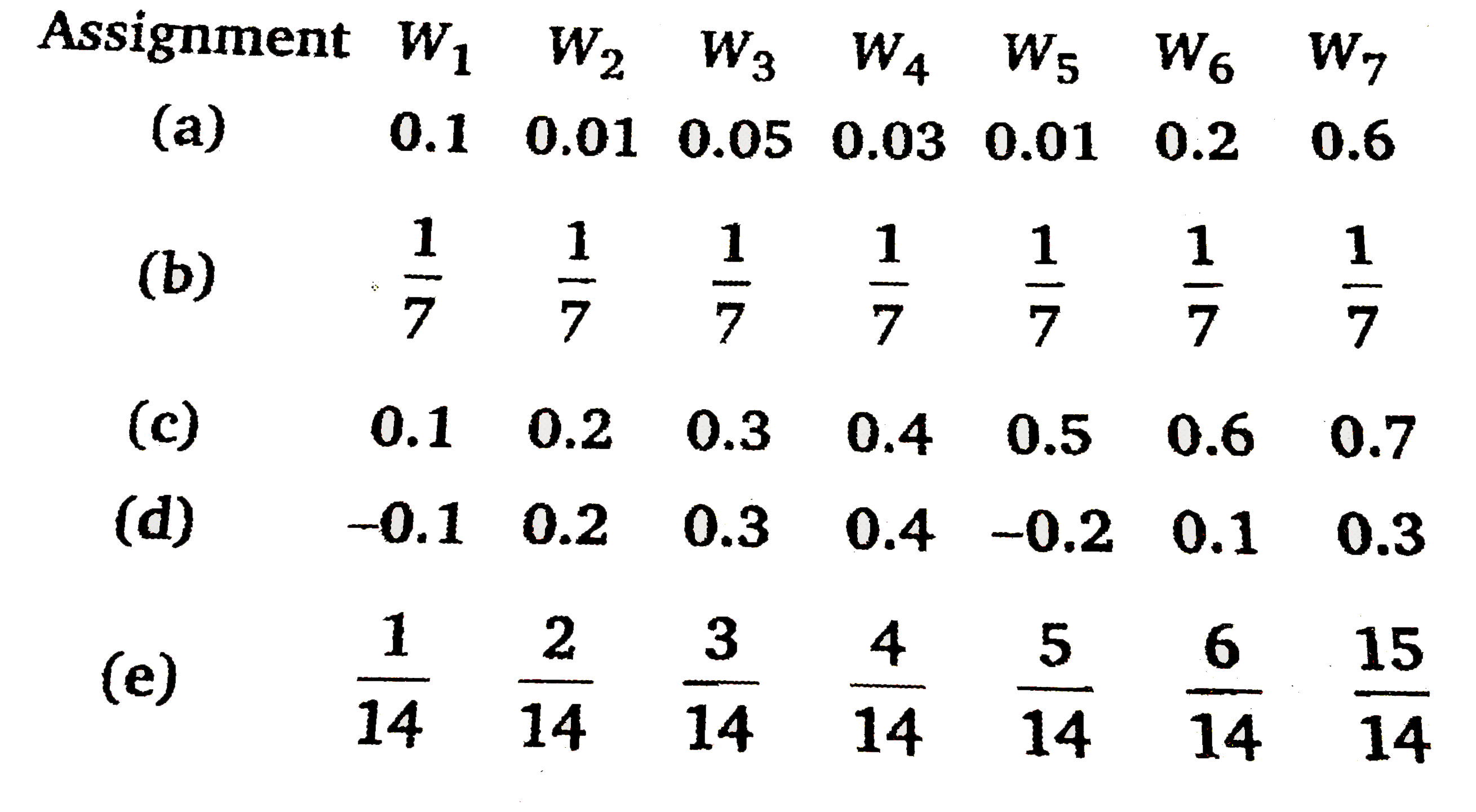 03:16View Solution
03:16View SolutionIf two events A and B are such that P(Al)=0.3, P(B)=0.4 and P(A∩Bl)=0.5, then P(BA∪Bl) equals
View SolutionA signal which can be green or red with probability 45and15 respectively, is received by station A and then and 3 transmitted to station B. The probability of each station receiving the signal correctly is 34 If the signal received at station B is green, then the probability that the original signal was green is (a) 35 (b) 67 (c) 2023 (d) 920
02:52View SolutionA bag contains 50 tickets numbered 1,2,3..., 50 of which five are drawn at random and arranged in ascending order of magnitude (xz<x2<x3<x4<x5) .="" the="" probability="" that="" x3=30" (^(20)c2)=(^(50)c5)="" (b)="" (^2c2)=(^(20)c_2x^(29)c_2)="" (d)="" none="" of="" these
01:25View SolutionIf (xi,1xi),i=1,2,3,4 are four distinct points on a circle, then (A) x1x2=x3x4 (B) x1x2x3x4=1 (C) x1+x2+x3+x4=1 (D) 1x1+1x2+1x3+1x4=1
05:04View SolutionFrom a bag containing 30 tickets numbered 1, 2, 3, ... 30, three tickets are selected at random without replacement. Suppose these tickets are arranged as x1<x2<x3. The probability that x2 = 15 and x3>20, is
06:11View SolutionIf mean and standard deviation of 5 observations x1,x2,x3,x4 are 10 and 3 respectively , then the variance of 6 observation x1,x2,…..x5and−50 is equal to:
06:48View SolutionA bag contains 50 tickets numbered 1, ,2 3, ...50. Find the number of set of five tickets x1<x2<x3<x4<x5 and x3=30
05:46View SolutionA bag contains 50 tickets numbered 1, 2, 3, .., 50 of which five are drawn at random and arranged in ascending order of magnitude(x1<x2<x3<x4<x5) find the probability that x3=30.
03:03View SolutionA bag contains 50 tickets numbered 1, 2, 3, .., 50 of which five are drawn at random and arranged in ascending order of magnitude (x1<x2<x3<x4<x5) find the probability thatx3=30.
02:23View SolutionLet X be a random variable which assumes values x1,x2,x3, x4 such that 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4). Find the probability distribution of X.
04:39View SolutionLet X be a random variable which assumes values x1,x2,x3, x4
such that 2P(X=x1)=3P(X=x2)=P(X=x3)=5P(X=x4).
Find the probability distribution of X.02:32View SolutionA bag contains 30 tickets numbered from 1 to 30 . Five tickets are drawn at random and arranged in ascending order . Find the probability that the third number is 20.
(ii) a bag contains 50 tickets numbered 1,2,3 ……, 50 of which five are drawn at random and arranged in ascending order of magnitude (x1<x2<x3<x4<x5) . What is the probability that x3=30.?02:44View Solution

