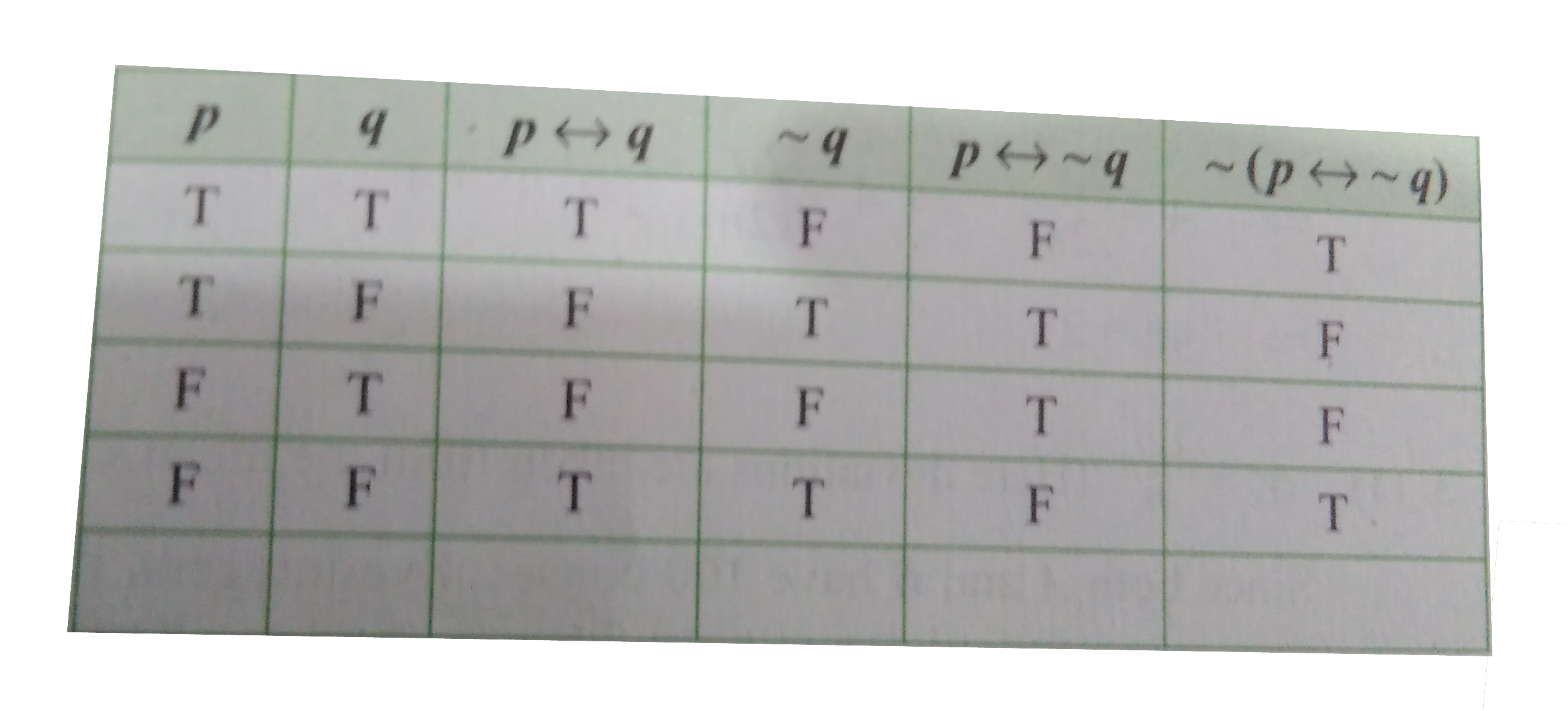Statement-1: ~(p↔~q) is equivalent to (p↔q).
Statement-2: ~(p↔~q) is a tautology.Solution in Tamil
Statement-1 is true, statement 2 is true, statement 2 is a correct explanation for statement 1
Statement 1 is true, statement-2 is true, statement 2 is not a correct explanation for statement 1
Statement 1 is true , statement 2 is false,
statement 1 is false, statement 2 is true
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
Which of the following is not a statement.
02:19View SolutionShow that the equation esinx−e−sinx−4=0 has no real solution.
03:09View SolutionIf A=⎡⎢⎣100101010⎤⎥⎦, then
02:47View SolutionThe statement ~(p↔~q) is (1) equivalent to p↔q (2) equivalent to ~p↔q (3) a tautology (4) a fallacy
View SolutionStatements -1 : ~(pharr~q) is equivalent to p harr q Statement-2: (~ p harr ~q) is a tautology.
07:17View SolutionThe statement ~(p↔~q) is
04:50View Solutionवक्तब्य I~(p⇔~q),p⇒q के तार्किक समतुल्य है
वक्तब्य II~(p⇔~q) एक पुनरुक्ति है05:37View SolutionSTATEMENT-1 : ~(p⇔q)=~p⇔q=p⇔~q
and
STATEMENT-2 : (p⇔q)⇔r=p⇔(q⇔r)04:06View SolutionThe statement ~(p⇔q) is not equivalent to
07:23View SolutionThe statement p⇔q is not equivalent to
02:33View SolutionThe statement (~(p⇔q))∧p is equivalent to
04:48View SolutionStatement-1: ~(p↔~q) is equivalent to (p↔q).
Statement-2: ~(p↔~q) is a tautology.02:09View SolutionStatement I ~(phArr ~q) ,phArr q K is the logical equivalent. Statement II ~(phArr ~q) There is a repetition.
04:01View SolutionStatements -1 : ~(pharr~q) is equivalent to p harr q Statement-2: ~( p harr ~q) is a tautology.
03:50View SolutionThe statement ~(p↔~q) is
05:12View SolutionStatements -1 : ~(pharr~q) is equivalent to p harr q Statement-2: (~ p harr ~q) is a tautology.
07:05View Solution