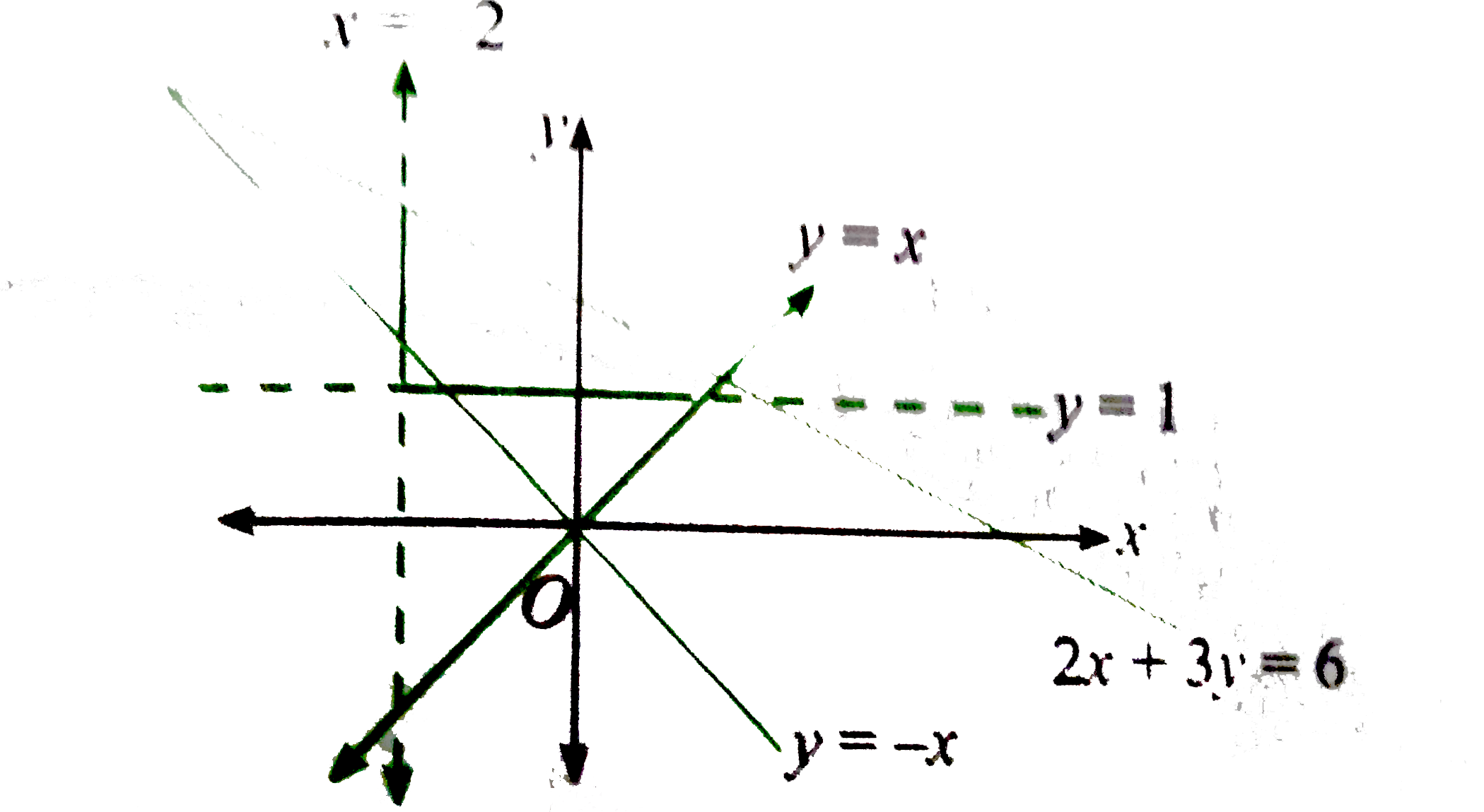
The combined equation of three sides of a triangle is $(x^{2} - y^{2}) (2 x + 3 y - 6) = 0$ . If $(- 2, a)$ is an interior point and $(b, 1)$ is an exterior point of the triangle, then (a) $2 < a < \frac{10}{3}$ (b) $- 2 < a < \frac{10}{3}$ (c) $- 1 < b < \frac{9}{2}$ (d) $- 1 < b < 1$

A

$2 < a < 10 / 3$

B

$- 2 < a < 10 / 3$

C

$- 1 < b < 9 / 2$

D

$- 1 < b < 1$

Text Solution

Verified by Experts

The correct Answer is:1,4

The separate equations of the sides are $x - y = 0, x + y = 0 and 2 x + 3 y - 6 = 0$ . The point (-2,a) moves on the line $x = - 2$ and the point (b,1) moves on the line $y = 1$ . From the figure , the y- coordinates of the points of intersection of $x = - 2$ with $y = - x and 2 x + 3 y = 6$ given the range of values of a . The x - coordinates of the points of intersection of $y = 1$ with $y = - x and y = x$ give the range of values of b.

|

Updated on:21/07/2023

Class 12 MATHS PAIR OF STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If the equation of the sides of a triangle are x + y = 2, y = x and $\sqrt{3} y + x = 0$ , then which of the following is an exterior point of the triangle?
AOrthocentre
BIncentre
CCentroid
DNone of these
Question 2 - Select One or More
If the equations of three sides of a triangle are $x + y = 1, 3 x + 5 y = 2 and x - y = 0$ then the orthocentre of the triangle lies on the line/lines
A $5 x - 3 y = 1$
B $5 y - 3 x = 1$
C $2 x - 3 y = 1$
D $5 x - 3 y = 2$

CENGAGE-PAIR OF STRAIGHT LINES-Exercise (Multiple)

Home
Ask Doubt
Profile