The number of solution of 2cosx=|sinx| where x∈[0.4π] is/areSolution in Tamil
To find the number of solutions to the equation 2cosx=|sinx|,0≤x≤4π, we need to find how many times the graphs of y=2cosxandy=|sinx| intersect in [0,4π].
The graphs of y=2cosxandy=|sinx| are plotted as ss
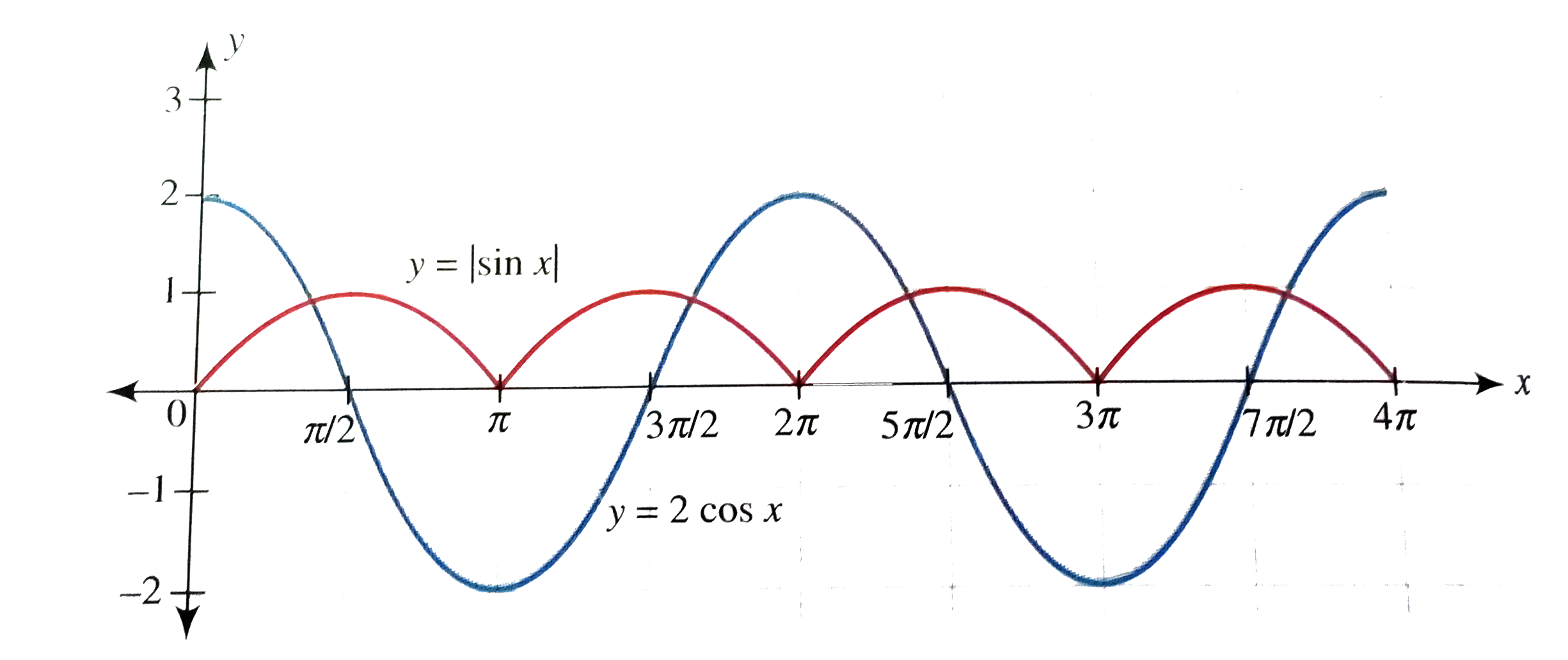
We find that the graphs intersect at four points. Hence the equation has four solutions.
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
14 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=tan−1x+cot−1x
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View Solution∫x2cosx(1+sinx)2dx
View SolutionThe number of solution of 2cosx=|sinx| where x∈[0.4π] is/are
View Solutionनिम्नलिखित समाकलनों के मान ज्ञात कीजिए-
∫exsinx(sinx+2cosx)dx
View Solutionx के सापेक्ष समाकलन कीजिए -
exsinx(sinx+2cosx)
View SolutionNumber of solutions of the equation sinx−sin2x+sin3x=2cos2x−2cosx is (0,π) is
View Solutionপ্রমাণ করো:∫sinx−cos2x1+sinxdx=−(x+2cosx)+c
View Solution∫ex(sinx+2cosx)sinxdx is equal to
View SolutionNumber of solutions of the equation, [y+[y]]=2cosx is: (where y=1/3)[sinx+[sinx+[sinx]]] and []= greatest integer function) 0 (b) 1 (c) 2 (d) ∞
View SolutionThe number of solution of 2cosx=|sinx| where x∈[0.4π] is/are
View Solutionसमीकरण [y+[y]]=2cosx के हलो की संख्या है-
(जहाँ y=(1/3)[sinx+[sinx]]] और []= महत्तम पूर्णाक फलन है।)
View SolutionNumber of solution of equation y=13[sinx+[sinx+[sinx]]] and [y+[y]]=2cosx is/are
View SolutionNumber of solutions of the equation, [y+[y]]=2cosx is: (where y=1/3)[sinx+[sinx+[sinx]]] and []= greatest integer function) (a). 0 (b) 1 (c) 2 (d) ∞
View Solution
