Solve graphically.Solution in Tamil
We have
Let us draw the graphs of .
The graph of is as follows.
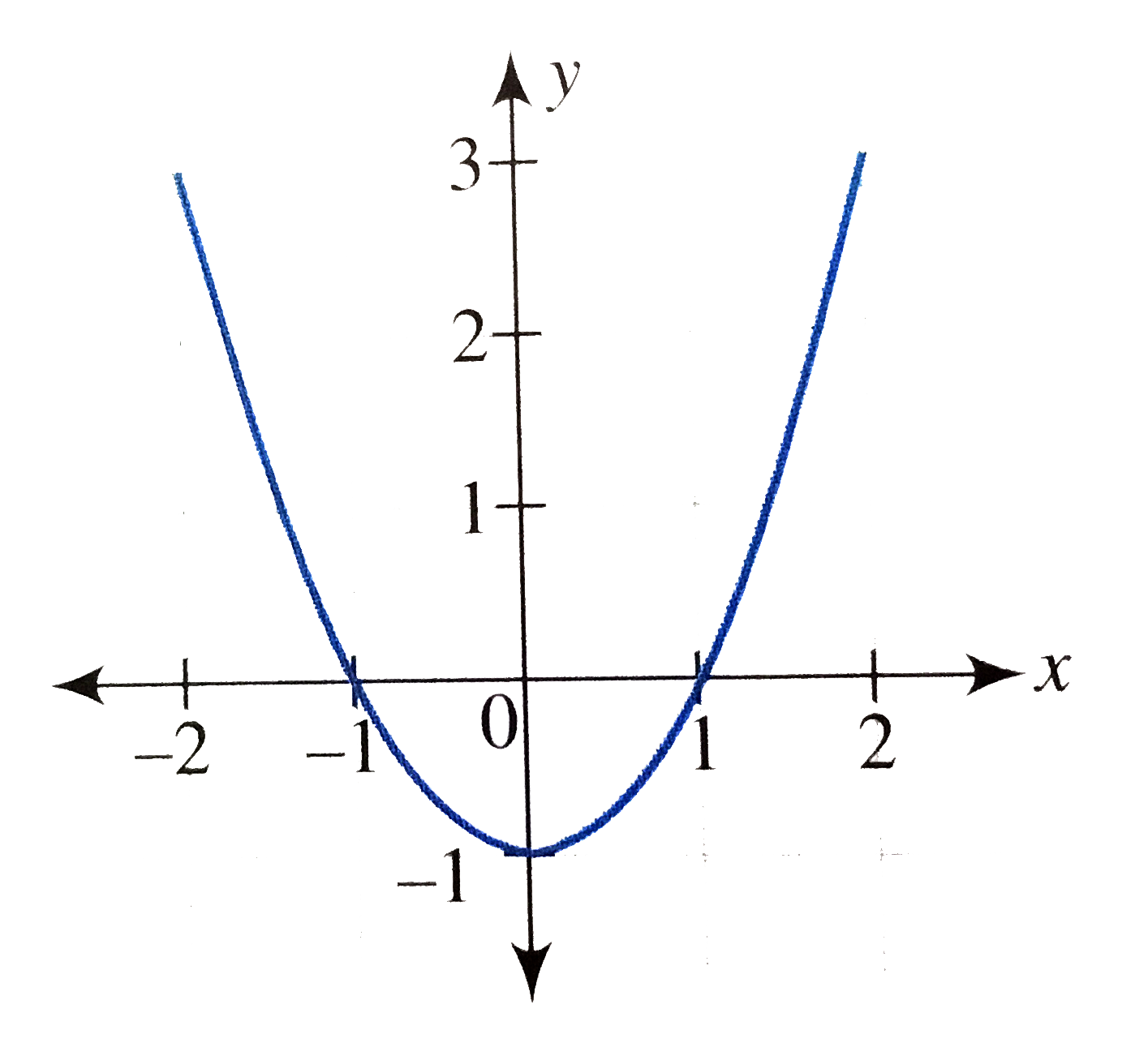
Graph of is as follows.
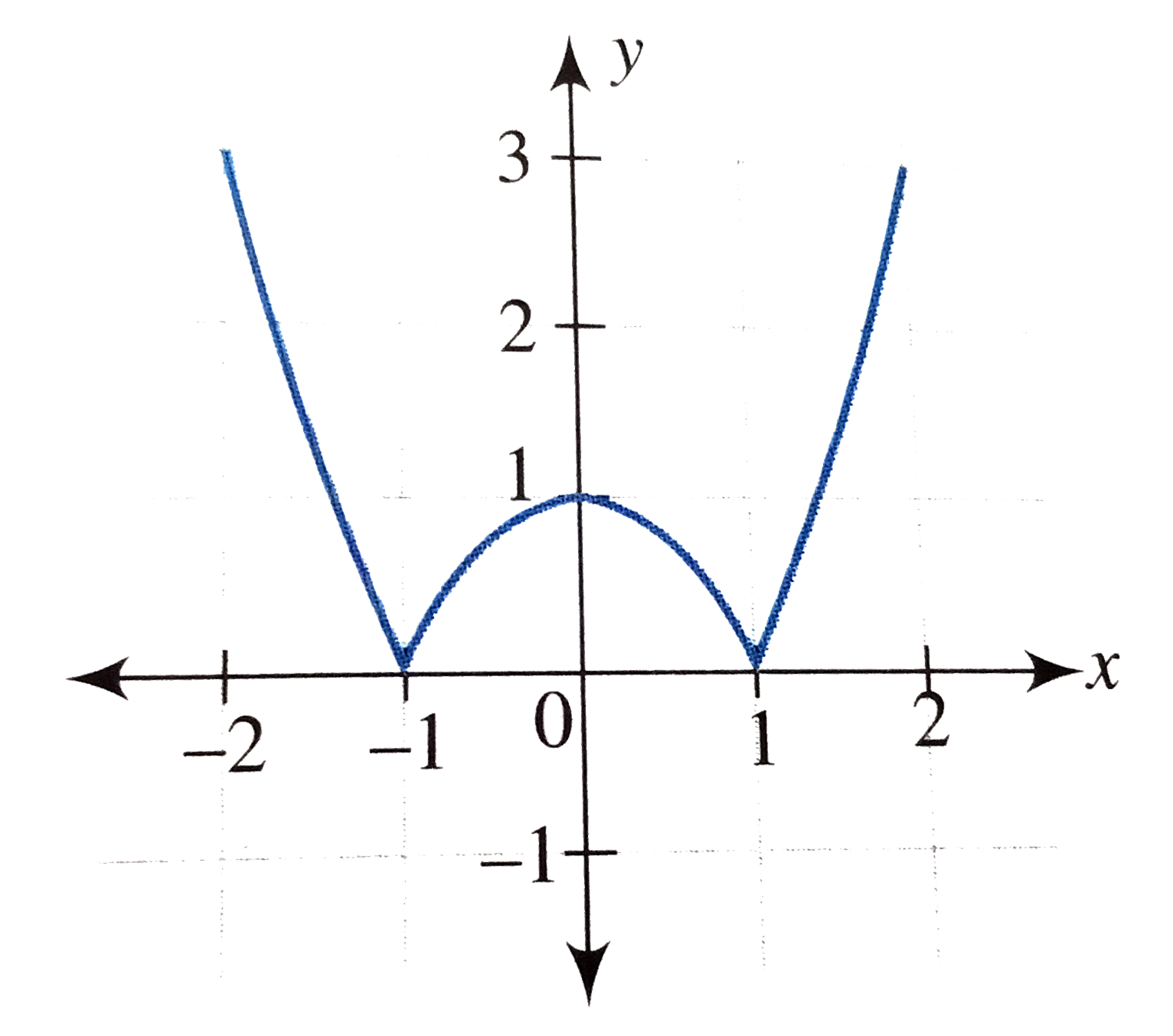
Graph of is as follows.
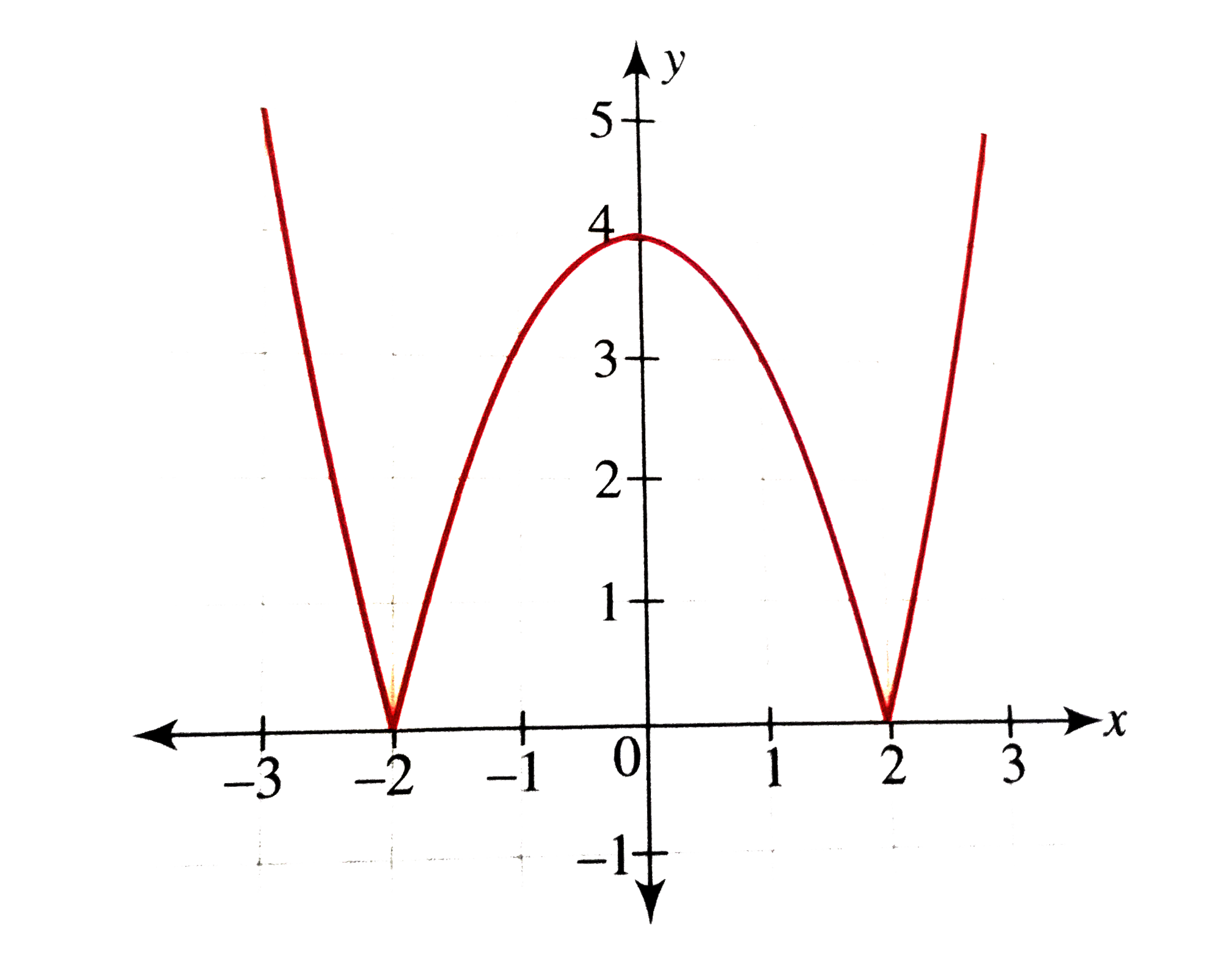
Garph of is as follows 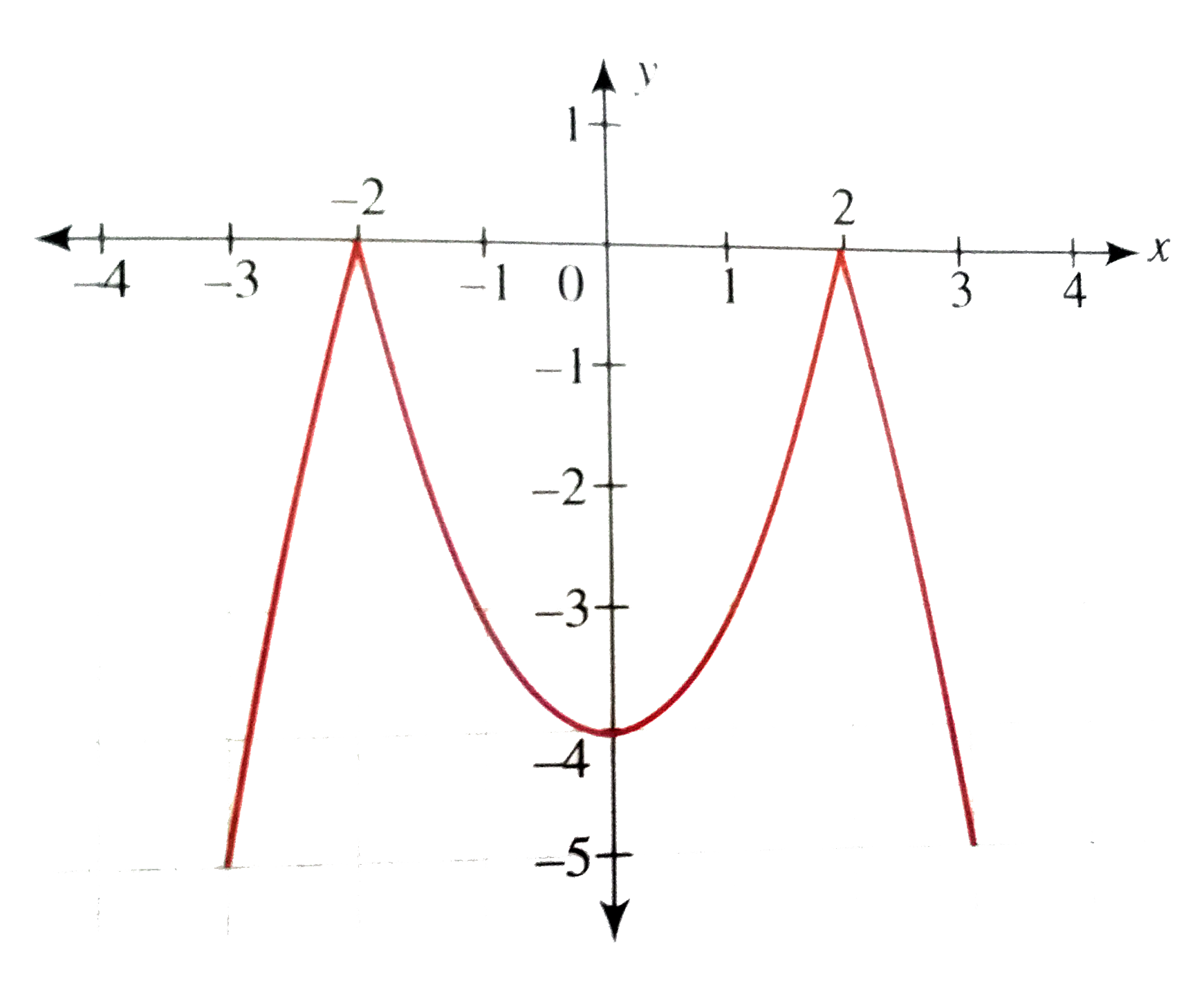
Graph of is as follows.
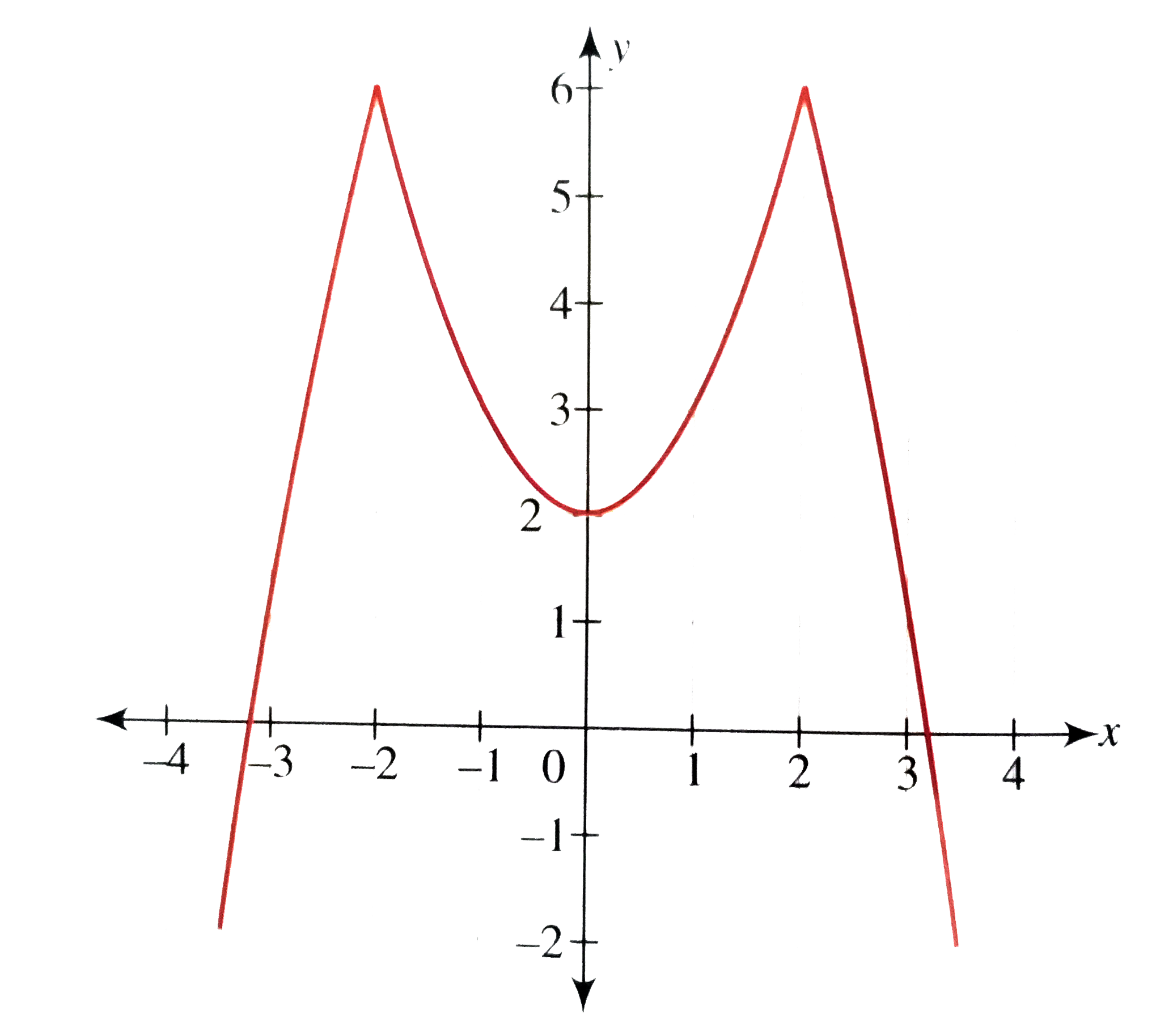
Graphs of are as shown in the following figure.

For the graph of lies below the graph of , the values of x lying between points A and B.
Solving for points of intersection, we have .
From the graph, the solution is .
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise14videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
03:06View SolutionDraw the graph of y=tan−1x+cot−1x
05:39View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=003:41View SolutionSOlve graphically y-1=x^(2)+|x|
05:17View SolutionSolve graphically y=[(x)/(2)]
03:24View SolutionSolve graphically y=(x+2)/(x-2)
02:20View SolutionSolve graphically y=2|x-2|-|x+1|+x
03:53View Solution|x|+2|y|=1 Solve graphically
02:20View Solutiony=max{x,x^(2)| Solve graphically
04:37View SolutionSolve |x−1|−|x+3|<6 graphically
04:13View SolutionSolve ∣∣x2−1∣∣+∣∣x2−4∣∣<6 graphically.
05:01View SolutionSolve graphically
x2+y4=1,x2+y4=204:31View Solution2x−34−2≥4x3−6 , 2(2x+3)<6(x−2)+10 , x∈R হলে রৈখিক অসমীকরণদ্বয়ের সমাধান হবে-
04:23View Solutionவரைபடமுறையில் தீர்க்க. x2+y4=1,x2+y4=2
07:17View SolutionSolve graphically x−y≤2
02:10View Solution

