Let be the perpendicular from the point to the plane. If makes an angle with the positive direction of the axis and makes an angle with the positive direction of axis, is the origin and are acute angels, then a. b. c. d. Solution in Tamil
, ,
, ,
, ,
, ,
The correct Answer is:B
If be then from the figure,
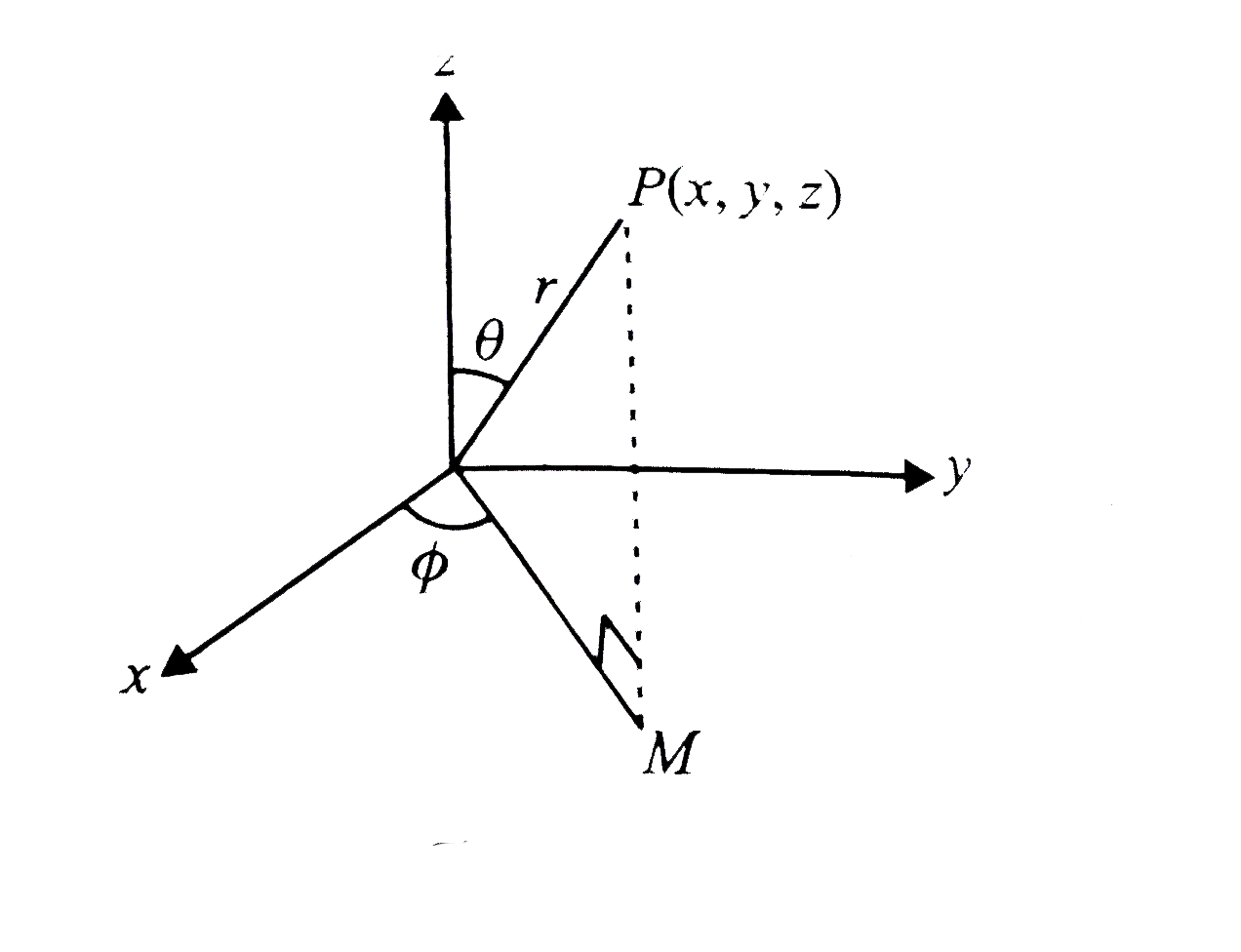
(neglecting negative sign as are acute)
Also, .
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Reasoning Questions)10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Comprehension)12videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Exercise (Single)86videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank12videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank4videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
Similar Questions
Statement 1 : Lines →r=ˆi−ˆj+λ(ˆi+ˆj−ˆk)and→r=2ˆi−ˆj+μ(ˆi+ˆj−ˆk) do not intersect.
Statement 2 : Skew lines never intersect.07:03View SolutionGiven four points A(2,1,0),B(1,0,1),C(3,0,1)andD(0,0,2). Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is02:38View SolutionIn a three-dimensional xyz space , the equation x2−5x+6=0 represents a. Points b. planes c. curves d. pair of straight lines
04:32View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
05:26View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]03:55View SolutionLet PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle ϕ with the positive direction of x− axis, whereO is the origin and θandϕ are acute angels, then a. cosθcosϕ=1/√14 b. sinθsinϕ=2/√14 c. tanϕ=2 d. tanθ=√5/3
03:55View SolutionIf O be the origin and OP=r and OP makes an angle θ with the positive direction of x-axis and lies in the XY plane find the coordinates of P.
04:04View SolutionLet PQ be the perpendicular form P(1,2,3) to xy-plane. If OP makes an angle theta with the positive direction of z-axis and OQ makes an angle ϕ with the positive direction of x-axis where O is the origin show that tanθ=√53andtanϕ=2.
07:18View SolutionLet PN be the perpendicular from the point
P(1,2,3) to xy-plane. If OP makes an angle α
with positive direction of the z-axis and ON makes
an angle β with the positive direction of x-axis,
where O is the origin (αandβ are acute angles),
then08:55View SolutionLet PM be the perpendicular from the point P(1,2,3) to XY-plane. If OP makes an angle θ with the positive direction of the Z-axies and OM makes an angle Φ with the positive direction of X-axis, where O is the origin, then find θandΦ.
05:21View SolutionLet PM be the perpendicular from the point P(1,2,3) to XY-plane. If OP makes an angle θ with the positive direction of the Z-axies and OM makes an angle Φ with the positive direction of X-axis, where O is the origin, θandΦ are acute angles, then
04:29View Solutionमाना O मूलबिंदु हैं तथा OP=r तथा OP, x अक्ष की धन दिशा से θ कोण बनाती हैं तथा XY तल में स्थित बिंदु 'P ' के निर्देशांक ज्ञात कीजिये|
02:50View SolutionLet PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle ϕ with the positive direction of x− axis, whereO is the origin and θandϕ are acute angels, then a. cosθcosϕ=1/√14 b. sinθsinϕ=2/√14 c. tanϕ=2 d. tanθ=√5/3
04:11View SolutionLet PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
11:41View Solutionयदि xy तल में बिन्दु P(1,2,3) से PM एक लम्ब हो, यदि −−→OP सदिश z-अक्ष की धनात्मक दिशा में कोण θ तथा −−→OM सदिश x. अक्ष की धनात्मक दिशा में कोण ϕ बनाते है, जहॉ O मूल बिन्दु और θ तथा ϕe न्यून कोण हों, तो
02:30View SolutionIf P≡(1,2,3) and O is origin, then direction cosines of OP are: a)1,2,3 b)−1,−2,−3 c)1√14,2√14,3√14 d)−1√14,2√14,3√14
06:20View Solution

