In R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?Solution in Tamil
2α+β+2γ+2=0
2α+β+2γ+4=0
2α+β+2γ−10=0
2α+β+2γ−8=0
The correct Answer is:B, D
b.,d
Clearly , planr P3isP2+λP1=0 .
⇒x+λy+z−1=0
Distance of this from point (0,1,0)is 1,
=0+λ+0−1√1+λ2+1=+1
∴λ=−12
thus , equation of P3is2x−y+2z−2=0
DIstance of this plane from point (α,β,γ)is 2.
=∣∣∣2α−β+2γ−23∣∣∣=2
⇒2α−β+2γ=2±6
thus options (b) and (d) are correct.
Topper's Solved these Questions
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - chapter-2
1 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - single correct answer type
1 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - matching column type
2 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
529 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Question Bank
17 Videos
Similar Questions
Let →u=u1ˆi+u2ˆj+u3ˆk be a unit vector in R3and→w=1√6(ˆi+ˆj+2ˆk) , Given that there exists a vector →v in R3 such that |→u×→v|=1and→w.(→u×→v)=1 which of the following statements is correct ?
View Solutionthe mirror image of point (3,1,7) with respect to the plane x−y+z=3 is P. then equation plane which is passes through the point P and contains the line x1=y2=z1.
View Solution
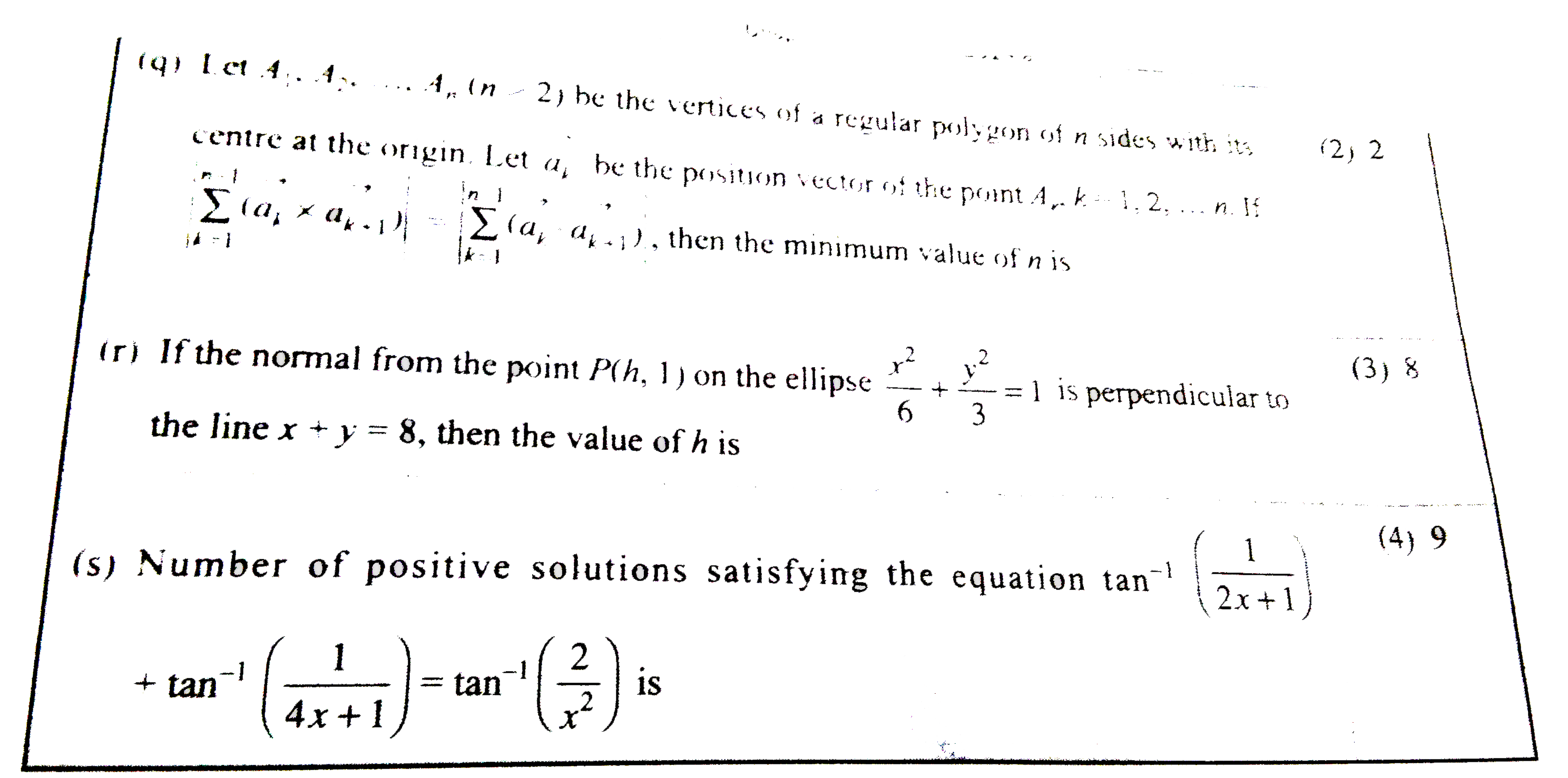
View SolutionFind x satisfying [tan−1x]+[cot−1x]=2, where [.] represents the greatest integer function.
View SolutionIf Limx→01−cosxeax−bx−1 exist and is equal to 1, then (a2+b2) equals
View SolutionLet P1=x+y+z+1=0,P2=x−y+2z+1=0,P3=3x+y+4z+7=0 be three planes. Find the distance of line of intersection of planes P1=0 and P2=0 from the plane P3=0.
View SolutionIn R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?
View SolutionLet P1:2x+y+z+1=0
P2:2x−y+z+3=0 and P3:2x+3y+z+5=0 be three planes, then the distance of the line of intersection of planes P1=0 and P2=0 from the plane P3=0 is
View SolutionIn R, consider the planes P1:y=0andP2:x+z=1. Let P3 be a plane, different from P1andP2, which passes through the intersection of P1andP2. If the distance of the point (0, 1,1) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relations is (are) true?
View Solutionमान लीजिए कि R3 में P1:y=0 और P2:x+z=1 दो समतल है। माना कि P3 एक समतल है जो समतल P1 और P2 से भिन्न है तथा P1 एवं P2 के प्रतिच्छेदन से जाता हैं यदि बिंदु (0,1,0) से P3 की दूरी 1 है। तथा बिंदु (α,β,γ) से P3 की दूरी 2 है तब निम्नलिखित संबंध (संबंधों) में कौन सा (से) संतुष्ट होते है?
View SolutionIn R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true? (a) 2α+β+2γ+2=0 (b) 2α−β+2γ+4=0 (c) 2α+β−2γ−10=0 (d) 2α−β+2γ−8=0
View SolutionIn R3, consider the planes P1:y=0 and P2,x+z=1. Let P3 be a plane, different from P1 and P2 which passes through the intersection of P1 and P2, If the distance of the point (0,1,0) from P3 is 1 and the distance of a point (α,β,γ) from P3 is 2, then which of the following relation(s) is/are true?
View Solutionमान लीजिए कि R3 में P1:y=0 और P2:x+z=1 दो समतल है। माना कि P3 एक समतल है जो समतल P1 और P2 से भिन्न है तथा P1 एवं P2 के प्रतिच्छेदन से जाता हैं यदि बिंदु (0,1,0) से P3 की दूरी 1 है। तथा बिंदु (α,β,γ) से P3 की दूरी 2 है तब निम्नलिखित संबंध (संबंधों) में कौन सा (से) संतुष्ट होते है?
View Solutionमान लीजिए कि R3 में P1:y=0 और P2:x+z=1 दो समतल है। माना कि P3 एक समतल है जो समतल P1 और P2 से भिन्न है तथा P1 एवं P2 के प्रतिच्छेदन से जाता हैं यदि बिंदु (0,1,0) से P3 की दूरी 1 है। तथा बिंदु (α,β,γ) से P3 की दूरी 2 है तब निम्नलिखित संबंध (संबंधों) में कौन सा (से) संतुष्ट होते है?
View SolutionLet P1:2x+y+z+1=0
P2:2x−y+z+3=0 and P3:2x+3y+z+5=0 be three planes, then the distance of the line of intersection of planes P1=0 and P2=0 from the plane P3=0 is
View Solution
