Question

Consider a pyramid OPQRS located in the first octant $(x\ge 0,y\ge 0,z\ge 0)$ with O as origin, and OP and OR along the x-axis and the y-axis,respectively. The base OPQR of the pyramid is asqu are with $OP=3$. The point S is directly above the mid-point T of diagonal OQ such that $TS=3$.Then

Options

A. the acute angle between OQ and OS is `pi //3`
B. the equataion of the plane containing th etriangle OQS is x-y=0
C. the length of the perpendicular from P to the plane containing the triagle OQS is `(3) /( sqrt(2))`
D. the perpendcular distance from O to the straight line containing RS is `sqrt((15)/(2))`

Answer

b.,c.,d

Explanation

b.,c.,d
Direction rations of`OQ-=(3,3,0)`
Direction rations of `OS-=((3)/(2),(3)/(2),3)`
if `theta` is the angle between OS and OR , then
`costheta=(3xx(3)/(2)+3xx(3)/(2))/(sqrt(3^(2)+3^(2))sqrt(((3)/(2))^(2)+((3)/(2))^(2)+3^(2)))=(1)/(sqrt(3))`

`therefore` hence (a) is wrong
Normal t plane OQS,
`vec(OQ)xxvec(OS)=+-|{:(hati,hatj,hatk),(3,3,0),((3)/(2),(3)/(2),3):}|=+-(9hati-9hatj)`
`therefore`Equation of plane OQS is
`(xhati+yhatj+zhatk).(9hati-9hatj)=0`
`implies x-y=0`
Distance of p from plane OQS = distancae PT = distance OT `=(3)/(sqrt(2))`
Equation of RS is `(x-0)/((3)/(2)-0)=(y-3)/((3)/(2)-3)=(z-0)/(3-0)`
`or (x)/((3)/(2))=(y-3)/(-(3)/(2))=(z)/(3)`

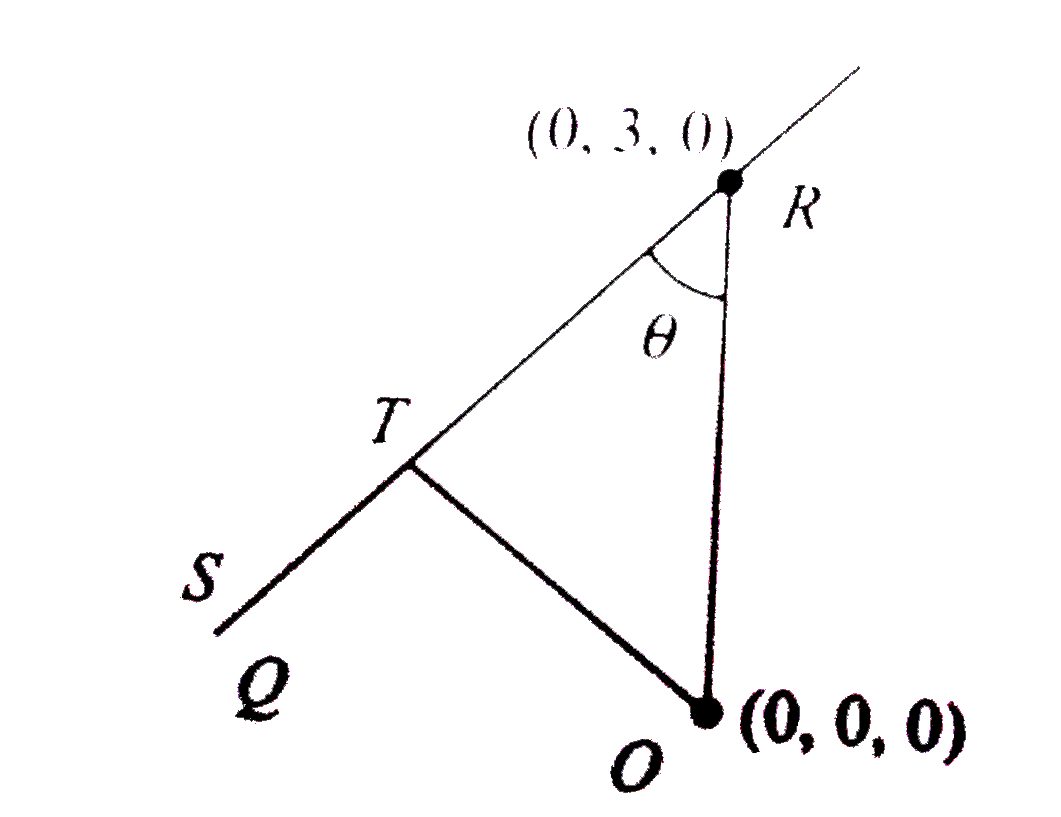
ANgle between line Rs and OR
`costheta=(0+3(-(3)/(2))+0)/(3sqrt(((3)/(2))^(2)+((3)/(2))^(2)+3^(2)))=-(1)/(sqrt(6))`
distance `= OT=ORsin theta=3sqrt(1-(1)/(6))=3sqrt((5)/(6))=sqrt((15)/(2))`