Let f(x)=xsinπx,x>0. Then for all natural numbers n,f′(x) vanishes at a unique point in the interval (n,n+12) a unique point in the interval (n+12,n+1) a unique point in the interval (n,n+1) two points in the interval (n,n+1)Solution in Tamil
We have f'(x)=sinπx+πxcosπx=0
⇒ tanπx=−πx
Now we draw the graphs of y=tanπx and y=−πx and look for their points of intersection. y=tanπx has period 1.
Graphs are as shown in the following figure.
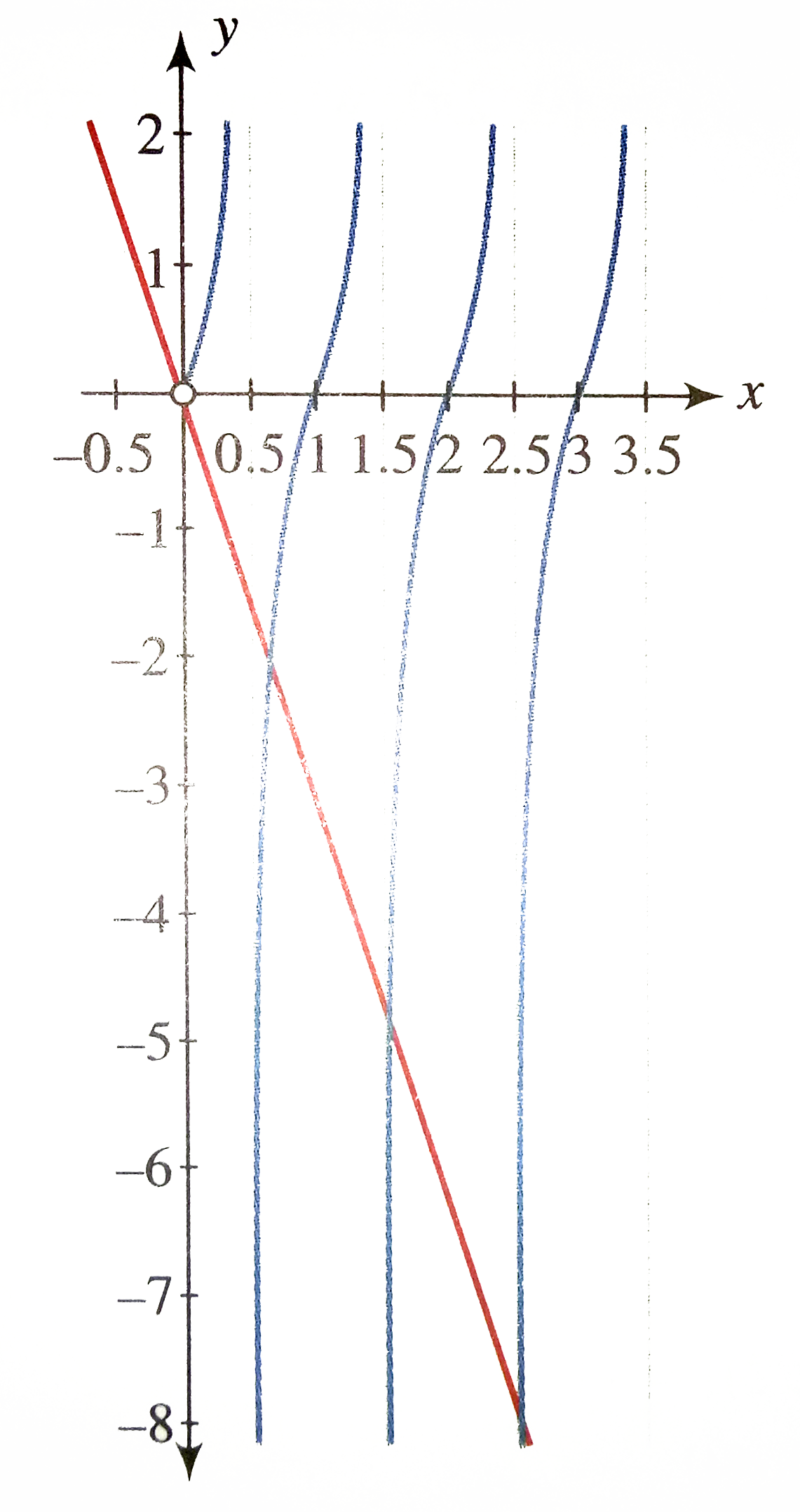
⇒ x∈(n+12,n+1)or(n,n+1)
Hence (b) and (c) are correct options.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year3videos
HIGHT AND DISTANCE
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
08:43View SolutionDraw the graph of y=1(1/x).
01:10View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
03:12View SolutionLet f(x)=xsinπx,x>0. Then for all natural numbers n,f′(x) vanishes at (A)a unique point in the interval (n,n+12) (B)a unique point in the interval (n+12,n+1) (C)a unique point in the interval (n,n+1) (D)two points in the interval (n,n+1)
05:45View SolutionIf f(x)=(a-x^(n))^((1)/(n)),a>0 and n in N, then prove that f(f(x))=x for all x.
01:30View SolutionThe interval [0, 4] is divided into n equal sub-intervals by the points x_0,x_1,x_2,....,x_(n-1),x_n where 0=x_0 0) sum_(i-1)^n x_i deltax is
03:33View SolutionLet f(x)=∣∣ ∣ ∣∣1/xlogxxn1−1/n(−1)n1aa2∣∣ ∣ ∣∣ where (wherefn(x)donotes nth derivative of f(x).
10:13View SolutionSuppose the function f(x)=xn,n≠0 is differentiable for all x. Then n can be any element of the interval
02:26View Solutionयदि a0n+1+a1n+a2n−1+...+an−12+an=0 तब सिद्ध कीजिए की अंतराल [0,1] में एक ऐसे x का अस्तित्व होगा जिसके लिए a0xn+a1xn−1+...+an=0
01:23View SolutionLet f(x)=(1+1x)x(x>0) and g(x)[xIn(1+(1/x)),if0<x≤1 0,ifx=0
limn→∞{f(1n).f(2n).f(3n)...f(nn)}1/nequals03:04View SolutionIf f(x)=1+xm(x−1)n,m,n∈N, then f'(x)=0 has atleast one root in the interval
08:36View SolutionIf f(x)=1+nx+n(n−1)2x2+n(n−1)(n−2)6x3+………………+xn, then f(1)=
02:17View SolutionLet f(x)=xsinπx,x>0. Then for all natural numbers n,f′(x) vanishes at (A)a unique point in the interval (n,n+12) (B)a unique point in the interval (n+12,n+1) (C)a unique point in the interval (n,n+1) (D)two points in the interval (n,n+1)
05:37View SolutionLet f(x)=xsinπx, x>0 . Then for all natural numbers n, f′(x) vanishes at (a) A unique point in the interval (n, n+12) (b) a unique point in the interval (n+12, n+1) (c) a unique point in the interval (n, n+1) (d) two points in the interval (n, n+1)
06:45View SolutionIf f(x)=(a−xn)1n,a>0andn∈N, then prove that f(f(x))=x for all x.
04:20View Solutionf(x) एक सतत् फलन है, जो एक संवृत्त अन्तराल [a,b] पर परिभाषित है, तब limn→∞n−1∑r=01nf(rn)=∫10f(x)dx
limn→∞1n{1n+1+2n+2+...+3n4n} का मान होगा04:09View Solution

