Question

Find the range of $f\left(x\right)=\left|\sin x\right|+\left|\cos x\right|,x\in R\stackrel{.}{}$

Explanation

We have ` y = f(x) = |sinx| + |cos x|, x in R`
Now `f(x + (pi)/(2)) = |sin(x + (pi)/(2))| + |cos (x + (pi)/(2))|`
`= |cos x| + | - sin x|`
`= |cos x| + |sin x|`
= f(x)
Thus, the period of `y = f(x) " is " (pi)/(2)`
We need to draw the graph of the function for `x in [0, (pi)/(2)]`
`f(x) = sin x + cos x = sqrt(2)sin((pi)/(4) + x) " for " x in [0, (pi)/(2)]`
`f(0) = f(pi//2) = 1, f((pi)/(4)) = sqrt2sin((pi)/(4) + (pi)/(4)) = sqrt(2)`
Also `f''(x) = sin x - cos x lt 0 " for " x in [0, (pi)/(2)]`
Therefore, the graph is concave downwards.
Hence the graph of `y = f(x) " for " x in [0, (pi)/(2)]` is as follows.

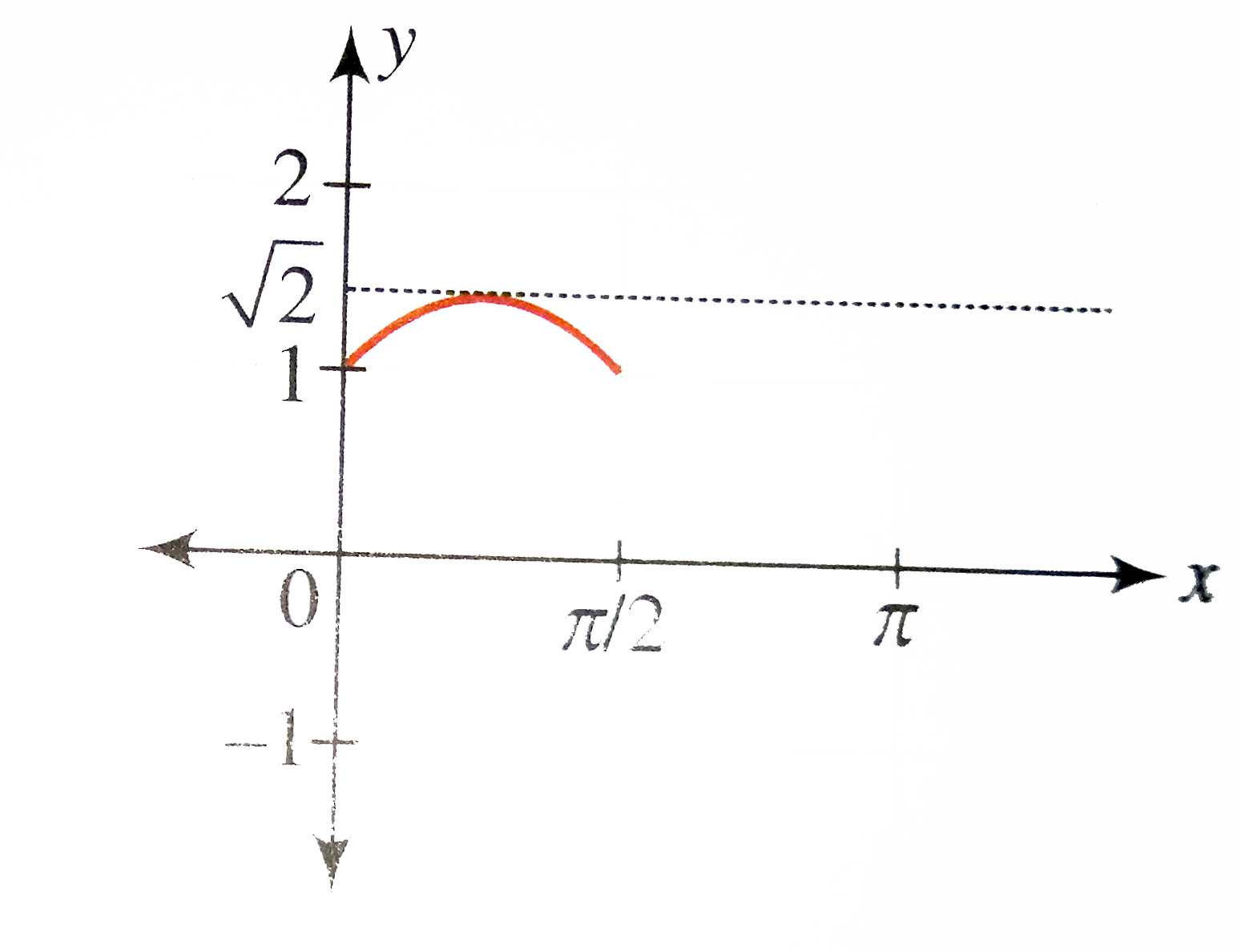
Since the period of `y = f(x) " is " pi//2`, the graph is repeated as shown in the following figure.

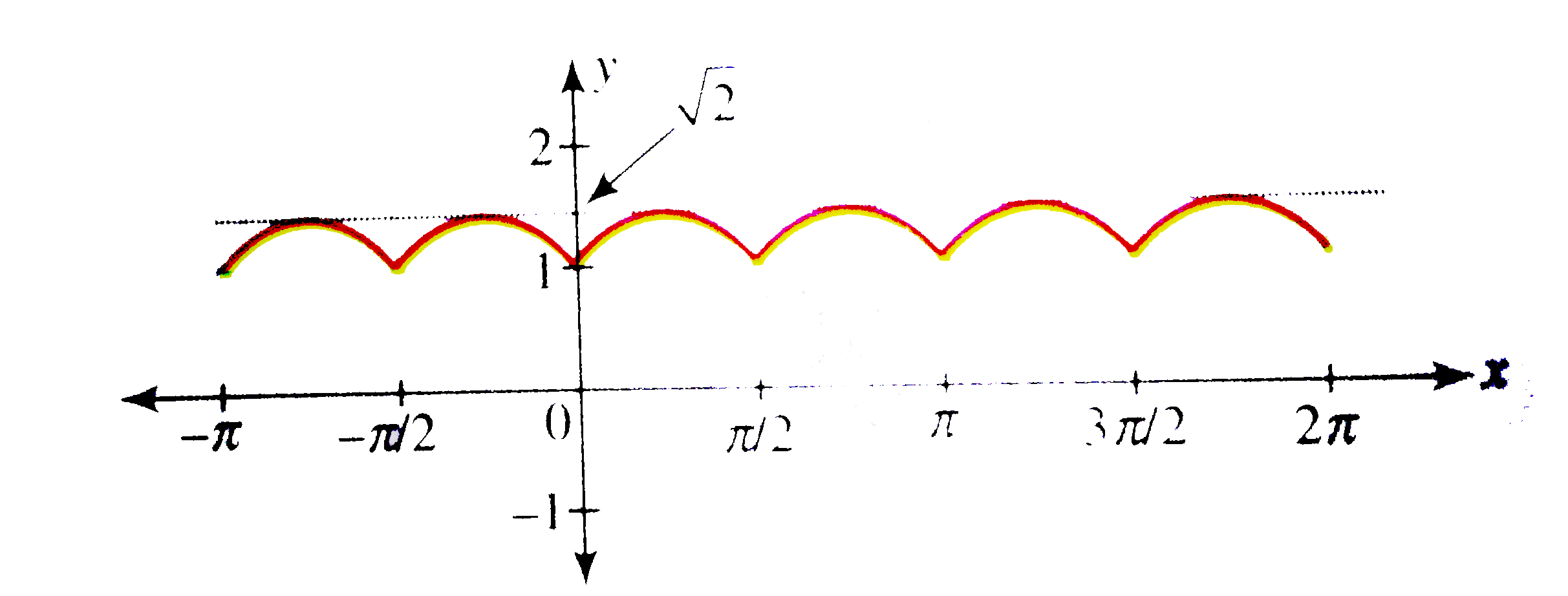
From the graph, the range of f(x) is `[1, sqrt(2)]`.