If f(x)=3√1−x2+3√1−x2,thenf(x) isSolution in Tamil
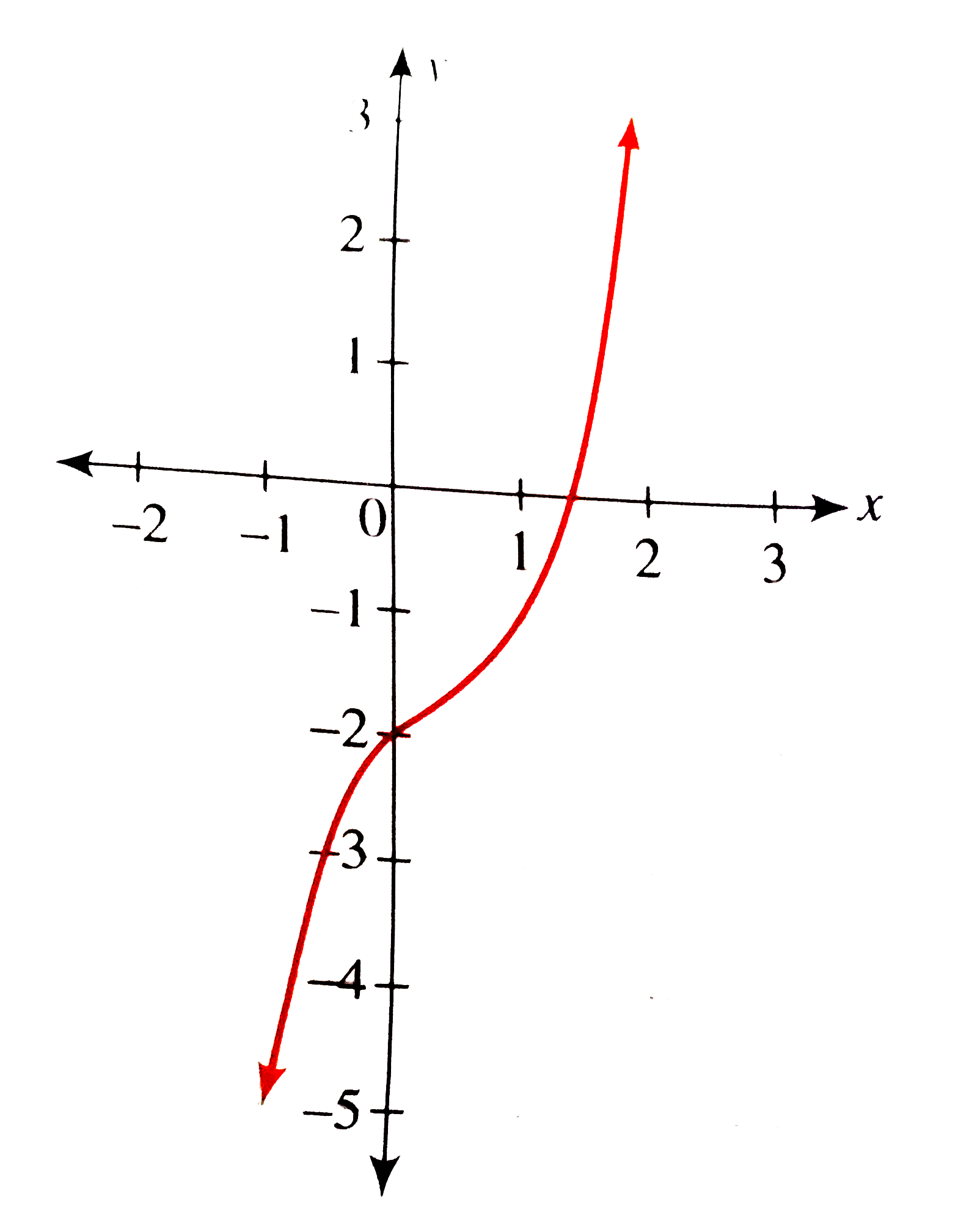
We have y=f(x)=x3−x2+x−2
dydx=3x2−2x+1>0,∀x∈R
So y=f(x) increases.
Since the leading coefficient is '3', when x→∞,f(x)→∞ and when x→−∞,f(x)→−∞.
f(0)=−2, hence the graph cuts the x-axis for some positive value of x.
Thus, the graph will cut the x-axis at one point only.
Also f(1)=−1 and f(2)=4.
Thus, the graph will cut the x-axis somewhere between '1' and '2'.
From the above discussion, the graph of y=f(x) can be drawn as shown in the following figure.
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
14 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=1(1/x).
View SolutionIf [3(3sqrt(x)-(1)/(3sqrt(x)))]^((1)/(3))=2 then find the value of 3sqrt(x)+(1)/(3sqrt(x))
View SolutionFind the range of f(x)=11−3√1−sin2x
View Solutionif f(x) is x^(2)-3sqrt(2x)-1 then find the vale of f(3sqrt(2))
View Solutionconsider a function f(x) Minimum distance between the functions f(x)and g(x) is 43√2 (b) 76√2 (c) 73√2 (d) 83√2
View SolutionConsider f:R rarr Rf(x)=3sqrt(x+sqrt(1+x^(2)))+3sqrt(x-sqrt(1+x^(2))) and its inverse be given by f^(-1)(x)=(x^(3)+ax)/(b)
View SolutionThe domain of f(x)=3sqrt(x)cot x is
View SolutionIf 3 ⎷3 ⎷x−13√x=2,then3√x+(13√x)=___________
View SolutionIf f(x)=3√5x, what is the value of f−1(15)?
View SolutionWhat is the domain of f(x)=3√15−x2?
View SolutionIf f(x)=√1+x−3√4−x, then f(x) is defined when x lies in
View SolutionExpand
(2x2−3√1−x2)4+(2x2+3√1−x2)4
View SolutionThe domain of the function f (x) = 3√x1−|x|
View Solution
