Let a ∈ R and f : R→R be given by f(x)=x5−5x+a, then
(a) f(x)=0 has three real roots if a>4
(b) f(x)=0 has only one real root if a>4
(c) f(x)=0 has three real roots if a<−4
(d) f(x)=0 has three real roots if −4<a<4Solution in Tamil
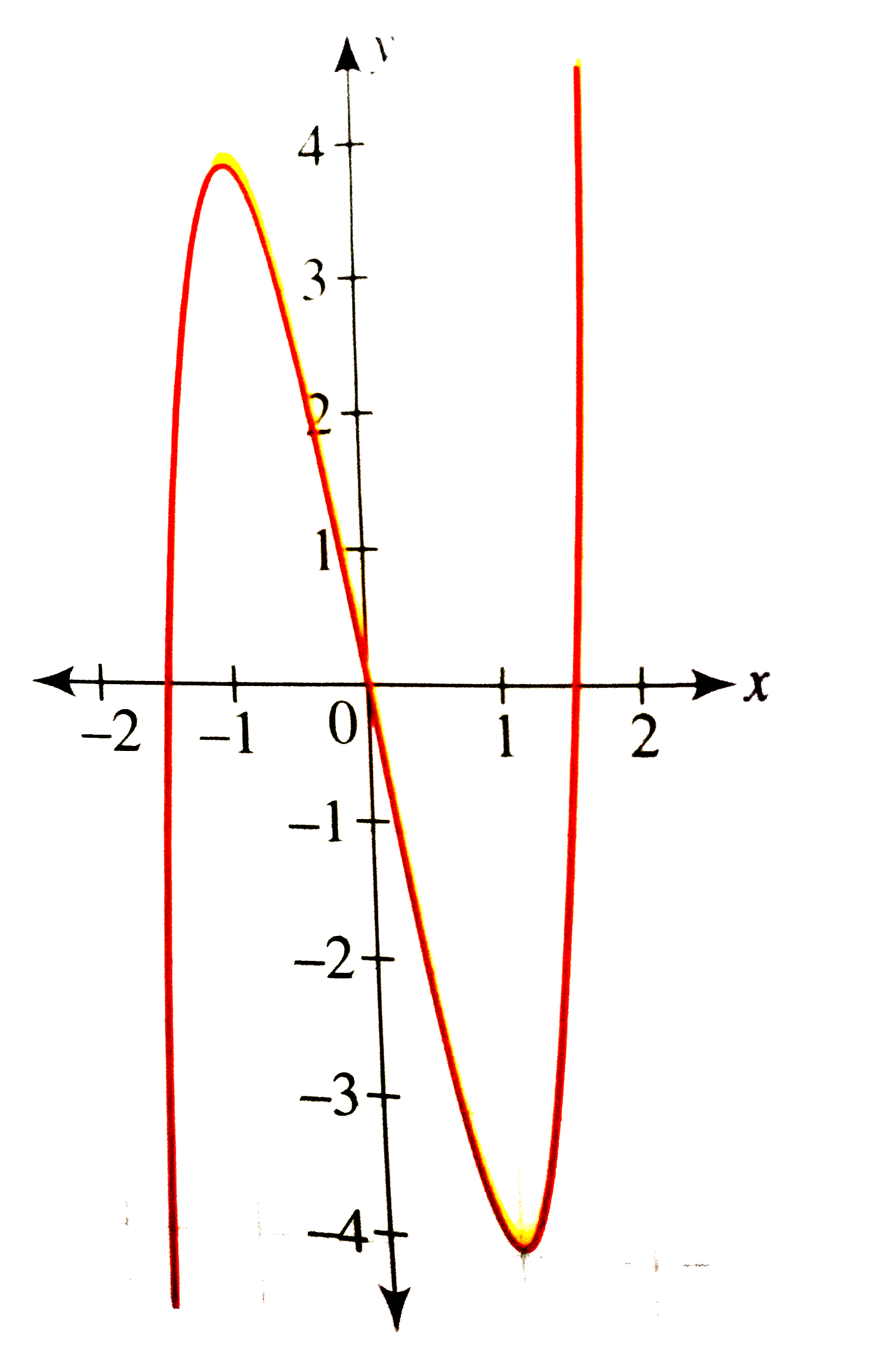
Let =f(x)=x5−5x
⇒f'(x)=5x4−5
=5(x4−1)
=5(x−1)(x+1)(x2+1)
f'(x)=0,∴x=−1,1
f''(x)=20x3
f''(1)=20 and f''(−1)=−20
So x = 1 is the point of minima and x = -1 is the point of maxima.
Also f(1)=−4 and f(−1)=4
Graph of y=f(x) is as shown in the adjacent figure.
From the graph, x5−5x=−a has one real root if −a<−4 or −a>4,
i.e. a>4 or a<−4
Also x5−5x=−a has three real roots if −4<−a<4
i.e. −4<a<4
Hence correct answers are (b) and (d).
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise14videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
03:51View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=004:16View SolutionDraw the graph of y=tan−1x−cot−1x.
02:34View SolutionDraw the graph of y=1(1/x).
06:07View SolutionIf f(x)=∫x8+4x4−2x2+2dx and f(0)=0,then (a)f(x) is an odd function (b)f(x) has range R (c)f(x) has at least one real root (d)f(x) is a monotonic function.
01:37View SolutionLate a∈R and let f:R→ be given by f(x)=x5−5x+a, then f(x) has three real roots if a>4 f(x) has only one real roots if a>4 f(x) has three real roots if a<−4 f(x) has three real roots if −4<a<4
03:17View SolutionIf f(x) is a polynomial of degree 5 with real coefficientssuch that f(|x|)=0 has 8 real roots,then the number of roots of f(x)=0
03:54View Solutionf(x) is a polynomial function, f:R→R, such that f(2x)=f'(x)f''(x). Equation f(x) = x has (A) three real and positive roots (B) three real and negative roots (C) one real root (D) three real roots such that sum of roots is zero
06:05View SolutionStatement I The equation f(x)=4x5+20x−9=0 has only one real root.
Statement IIf'(x)=20x4+20=0 has no real root.07:06View SolutionIf f(x) is a polynomial of degree 5 with real coefficients such that f(|x|)=0 has 8 real roots, then f(x)=0 has
03:58View SolutionIf f(x) is a real valued polynomial and f (x) = 0 has real and distinct roots, show that the (f'(x)^(2)-f(x)f''(x))=0 can not have real roots.
View SolutionLet a∈R and let f:R→ be given by f(x)=x5−5x+a, then (a) f(x) has three real roots if a>4 (b)f(x) has only one real roots if a>4 (c)f(x) has three real roots if a<−4 (d)f(x) has three real roots if −4<a<4
05:01View Solutionf(x) is a polynomial function, f:R→R, such that f(2x)=f'(x)f''(x). Equation f(x) = x has (A) three real and positive roots (B) three real and negative roots (C) one real root (D) three real roots such that sum of roots is zero
12:55View SolutionStatement I The equation f(x)=4x5+20x−9=0 has only one real root.
Statement IIf'(x)=20x4+20=0 has no real root.03:56View SolutionA function f(x) is such that f(x)=0 has 8 distinct real roots and f(x)=f(6−x) for x∈R. Sum of real roots of the equation f(x)=0 is
02:15View SolutionLate a in R and let f: Rvec be given by f(x)=x^5-5x+a , then f(x) has three real roots if a >4 f(x) has only one real roots if a >4 f(x) has three real roots if a<-4 f(x) has three real roots if -4
02:24View Solution

