Let f(x)=x3−3x2+6∀x∈R and g(x)={max:f(t;x+1≤t≤x+2,−3≤x≤01−x,x≥ .Find continuity and differentiability of g(x) for x in [-3,1]Solution in Tamil
f(x)=x3−3x2+6
If f'(x)=3x2−6x=0, then x=0,2 are the critical points of f(x).
x=0 is the point of local maxima and x=2 is the point of local minima.
Clearly, f(x) is increasing in (−∞,0) and (2,∞) and decreasing in (0,2).
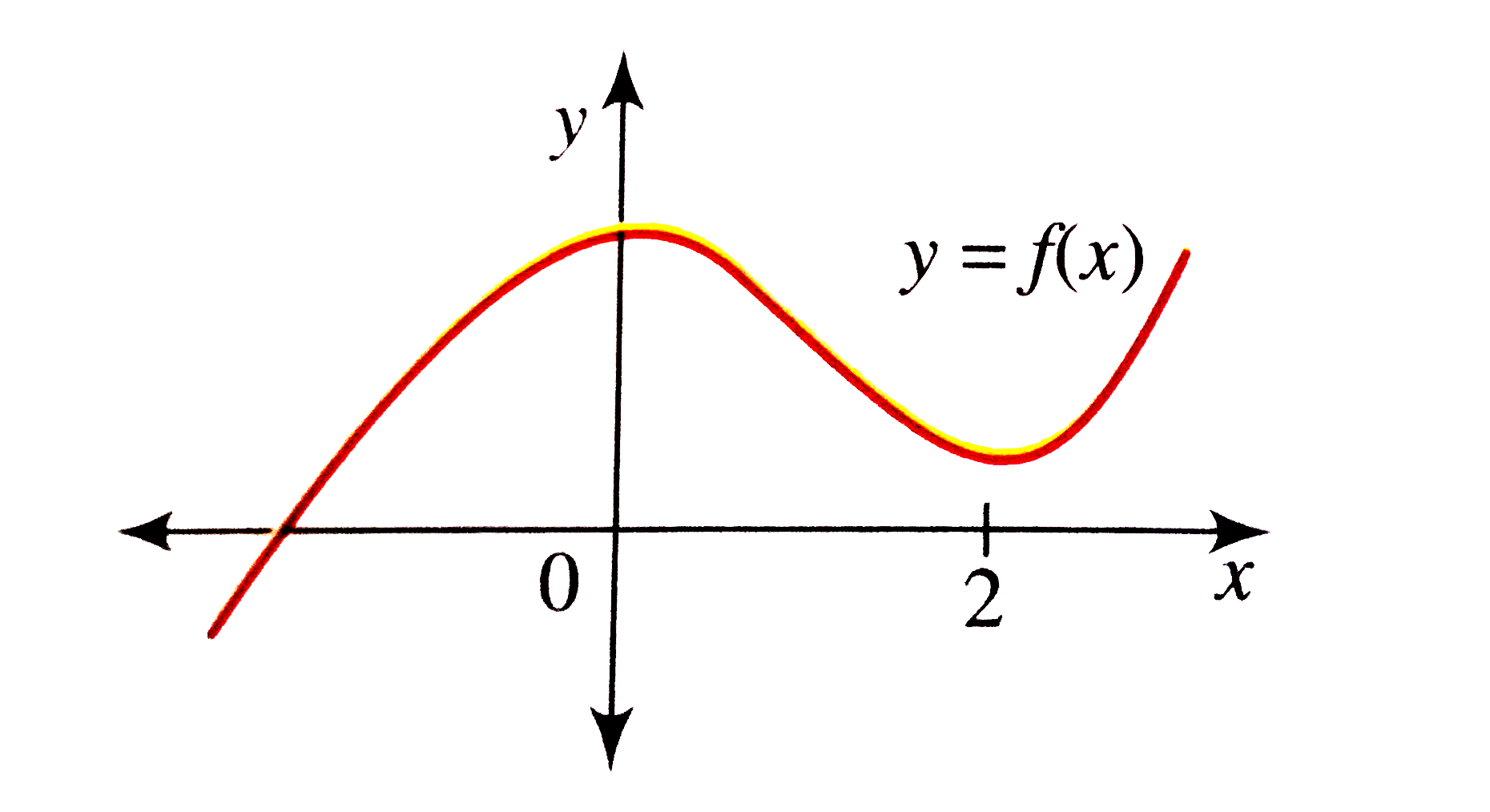
Case 1 : x+2≤0⇒x≤−2
⇒ g(x)=f(x+2),−3≤x≤−2
Case 2: x+1<0 and 0<x+2<2
x<−1 and −2<x<0
i.e., −2<x<−1 ∴g(x)=f(0)
Case 3: 0≤x+1,x+2≤2
⇒−1≤x≤0,g(x)=f(x+1)
⇒g(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩f(x+2), −3≤x<−2f(0), −2≤x<−1f(x+1), −1≤x<01−x, 0≤x<1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise14videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
05:53View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=004:28View SolutionDraw the graph of y=tan−1x−cot−1x.
05:47View SolutionDraw the graph of y=1(1/x).
05:45View Solutionf(x)={|x+1|;x≤0x;x>0 and g(x)={|x|+1;x≤1−|x−2|;x>1 Draw its graph and discuss the continuity of f(x)+g(x).
04:07View SolutionLet f(x)=x3−3x2+6∀x∈R and g(x)={max:f(t;x+1≤t≤x+2,−3≤x≤01−x,x≥
07:06View SolutionF(x)=x^(3)-3x^(2)+6 and g(x)=max{F(t):x+1 =0 Find continuity and differentiability of g(x) for x in[-3,1]
04:42View SolutionLet f(x)=|x-1|+|x-2| and g(x)={min{f(t):0<=t<=x,0<=x<=3 and x-2,x then g(x) is not differentiable at
05:38View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x for all x∈R. Then, h'(1) equals.
02:35View SolutionIf f(x)={x−3,x<0x2−3x+2,x≥0and letg(x)=f(|x|)+|f(x)|. Discuss the differentiability of g(x).
05:57View SolutionLet f(x) be continuous in a neighbourhood of 'a' and g(a)≠0 g is continuous at x=a. Let f be a function such that f'(x)=g(x)(x−a)2, then :
04:14View Solutionf(x)={|x+1|;x≤0x;x>0 and g(x)={|x|+1;x≤1−|x−2|;x>1 Draw its graph and discuss the continuity of f(x)+g(x).
11:33View SolutionLet f(x)={x+1,x>0,2−x,x≤0 and g(x)={x+3,x<1,x2−2x−2,1≤x<2,x−5,x≥2 Find the LHL and RHL of g(f(x)) at x=0 and, hence, fin limx→0g(f(x)).
07:10View SolutionLet f(x)=x3−3x2+6∀x∈R and g(x)={max:f(t;x+1≤t≤x+2,−3≤x≤01−x,x≥
06:09View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x for all x∈R. Then, h'(1) equals.
06:12View SolutionIf f(x)={x−3,x<0x2−3x+2,x≥0and letg(x)=f(|x|)+|f(x)|. Discuss the differentiability of g(x).
09:11View Solution

