Question

Draw the graph of ${\displaystyle y=\frac{1-x^2}{1+x^2}}$ and hence draw the graph of ${\displaystyle y={\cos }^{-1}.\frac{1-x^2}{1+x^2}}$.

Explanation

We have `y=f(x)=(1-x^(2))/(1+x^(2))=(2)/(1+x^(2))-1`
Clearly, the domain is R.
`y=f(x)` is an even funtion, so the graph is symmetrical about the y-axis.
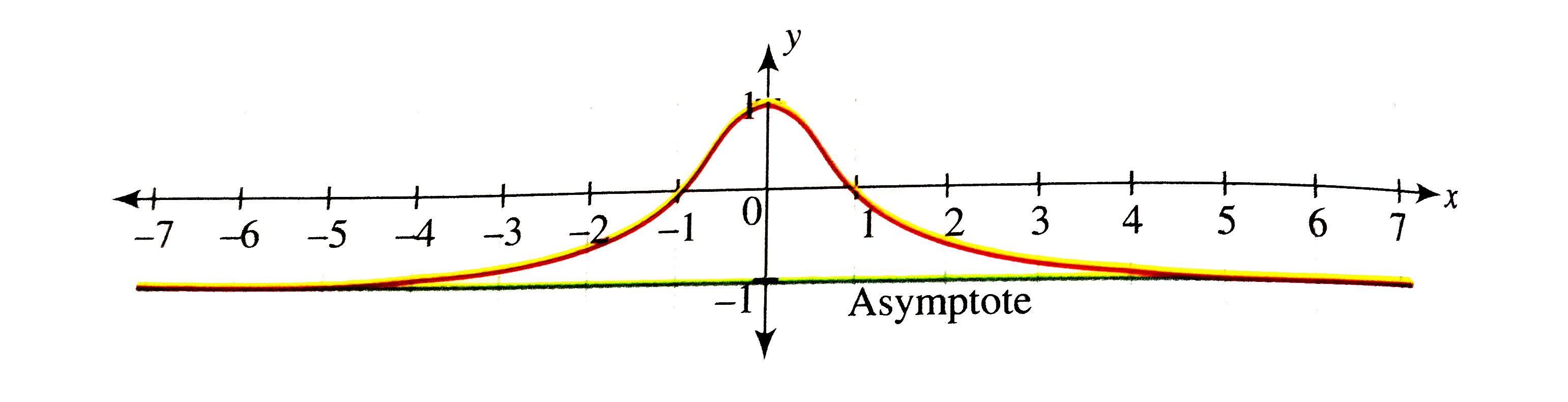
Let us first draw the graph of r`x in [0,oo)`.
`f(0)=1`
`f(x)=0 :. x=1`
`underset(xrarroo)lim((2)/(1+x^(2))-1)=-1`
Thus, from `f(0)=1,((2)/(1+x^(2))-1)` decreases intersecting the x-axis at (1,0) and approaches '-1' as x approaches `'oo'`.
Also `f'(x)=(-4x)/((1+x^(2))^(2))`, so f(x) is differentiable at x = 0.
Hence the graph of `y=f(x)` is as shown in the following figure.

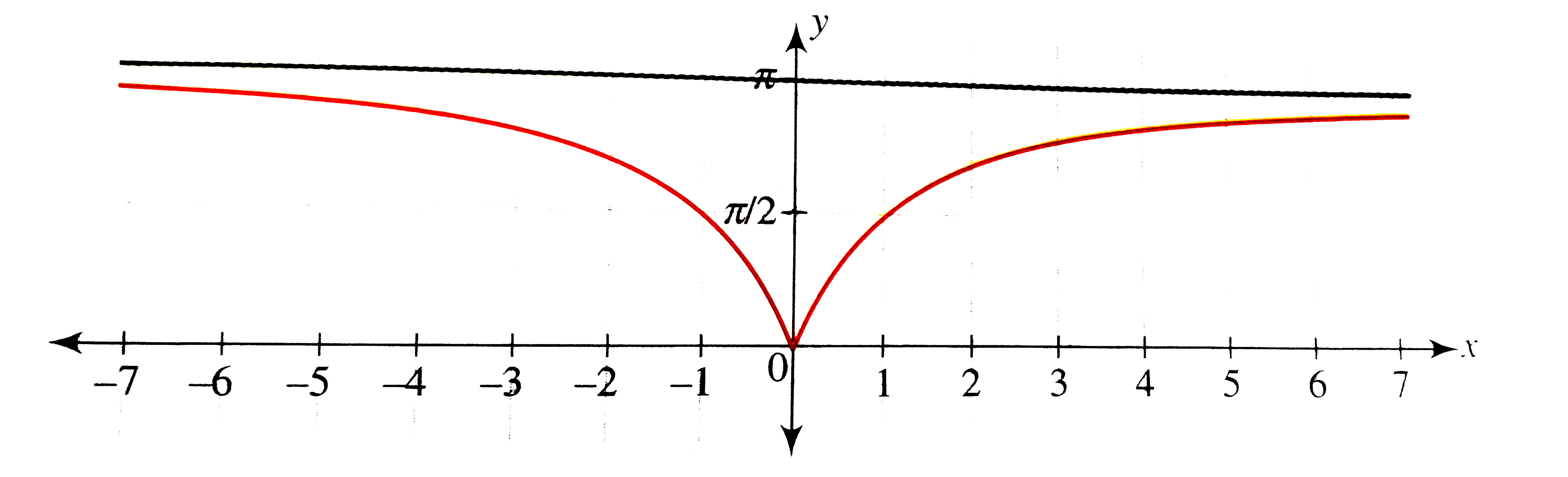
Since the range of `(1-x^(2))/(1+x^(2))` is (-1,1), the domain of `g(x)=cos^(-1)f(x)=cos^(-1).(1-x^(2))/(1+x^(2))` is also R
`g(0)=cos^(-1)(1)=0`
and `underset(xrarroo)limcos^(-1)((1-x^(2))/(1+x^(2)))=underset(xrarroo)lim cos^(-1)((2)/(1+x^(2))-1)=pi`
Thus, the value of g(x) increases from '0' and approaches `'pi'` as x approaches `'oo'`.
Also g(x) is an enven function, so the graph is symmetrical about the y-axis.
Also `g'(x)=(f'(x))/(sqrt(1-(f(x))^(2)))`
g'(0) does not exist as f(0)=1, so g(x) is non-differentiable at x=0.
Hence the graph of `y=g(x)` can be drawn as shown in the following figure.