If x2+2ax+a<0∀x∈[1,3], the find the values of a.Solution in Tamil
x2+2ax+a<0,∀x∈[1,2]
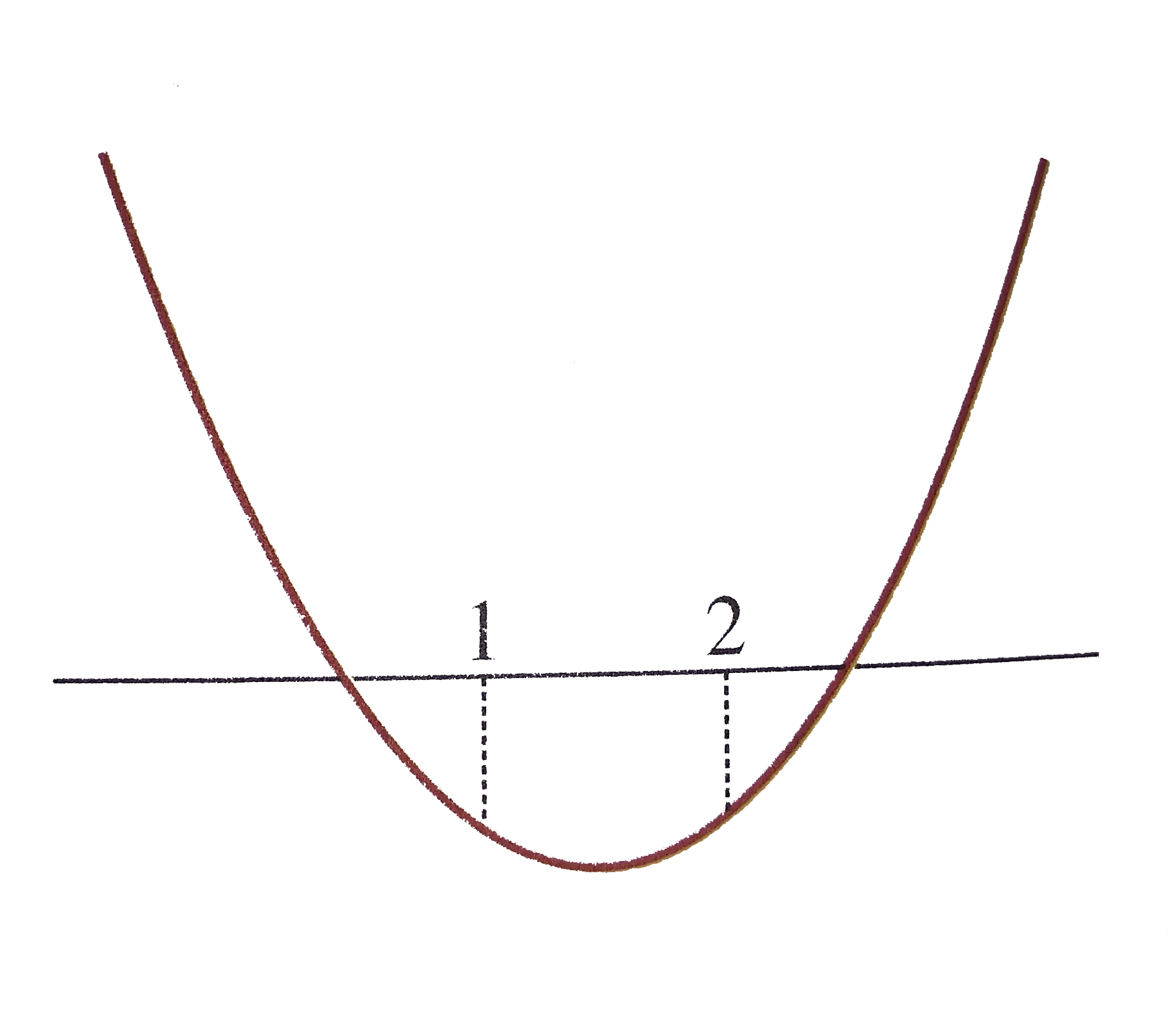
1 and 2 lie between the roots of the equation x2+2ax+a=0
⇒ f(1)<0andf(2)<0
⇒ 1+2a+a<0,4+4a+a<0
⇒ a<−13,a<−45
⇒ a∈(−∞,−45)
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionIf the equation asinx+cos2x=2a−7 possesses a solution, then find the value of a.
View SolutionIf the function f(x)=x2−(A+2)x+Ax−2,forx≠2andf(2)=2, is continuous at x=2, then find the value of A.
View SolutionLet a>2 be a constant. If there are just 18 positive integers satisfying the inequality (x−a)(x−2a)(x−a2)<0, then find the value of a.
View SolutionLet a>2 be a constant. If there are just 18 positive integers satisfying the inequality (x−a)(x−2a)(x−a2)<0, then find the value of a.
View SolutionFind the greatest value of f(x)12ax−x2−5a2∈[−3,5] depending upon the parameter a.
View SolutionIf x2+2ax+a<0∀x∈[1,2], the find the values of a.
View SolutionIf x2+y2−2x+2ay+a+3=0 represents the real circle with nonzero radius, then find the values of a.
View SolutionIf 2ax−2y+3z=0,x+ay+2z=0,and2+az=0 have a nontrivial solution, find the value of a.
View SolutionFor the function f(x)=(x2+bx+c)3xandg(x)=(x2+bx+c)3x+3x(2x+b). Which of the following holds goods? If f(x)>0∀x∈R⇒g(x)>0∀x∈R If f(x)>0∀x∈R⇒g(x)<0∀x∈R If g(x)>0∀x∈R⇒f(x)>0∀x∈R If g(x)>0∀x∈R⇒f(x)<0∀x∈R
View SolutionIf the equation asinx+cos2x=2a−7 possesses a solution, then find the value of a.
View SolutionIf the function f(x)=x2−(A+2)x+Ax−2,forx≠2andf(2)=2, is continuous at x=2, then find the value of A.
View SolutionLet a>2 be a constant. If there are just 18 positive integers satisfying the inequality (x−a)(x−2a)(x−a2)<0, then find the value of a.
View Solution
