If $(b_{2} - b_{1}) (b_{3} - b_{1}) + (a_{2} - a + 1) (a_{3} - a_{1}) = 0$ , then prove that the circumcenter of the triangle having vertices $(a_{1}, b_{1}), (a_{2}, b_{2})$ and $(a_{3}, b_{3})$ is $(\frac{a_{2 + a_{3}}}{2}, \frac{b_{2 +} b_{3}}{2})$ Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Given $(b_{2} - b_{1}) (b_{3} - b_{1}) + (a_{2} - a_{1}) (a_{3} - a_{1}) = 0$

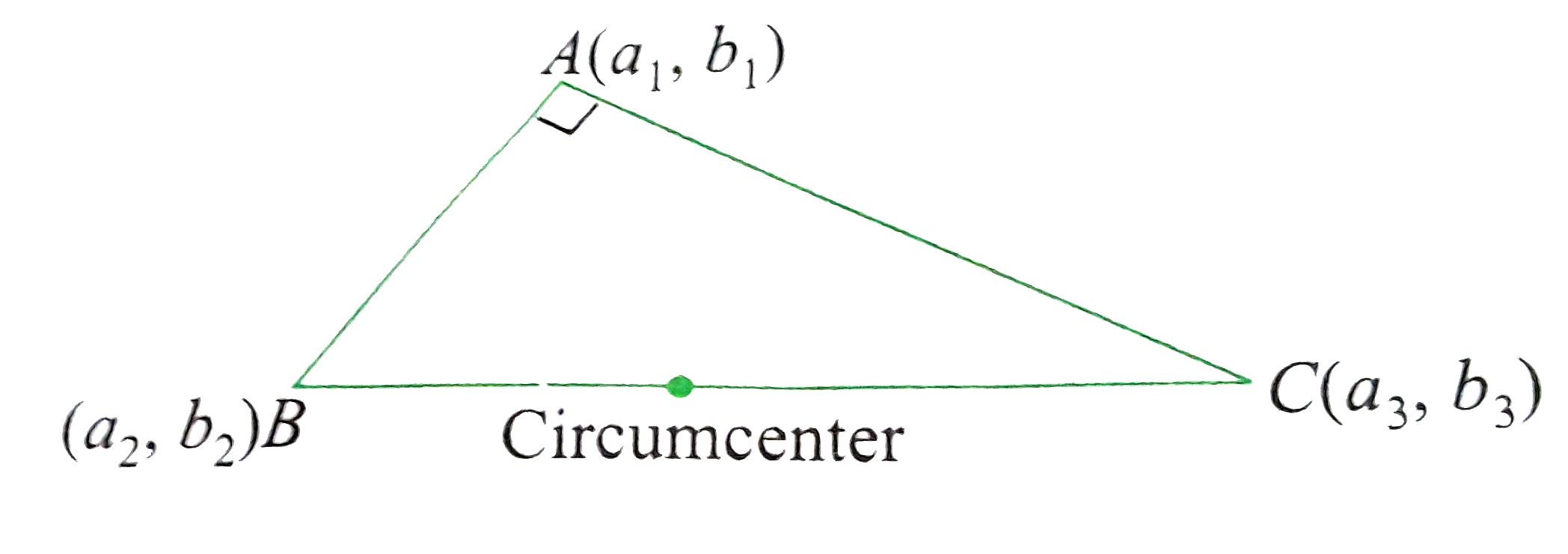
or $(b_{2} - b_{1}) (b_{3} - b_{1}) = - (a_{2} - a_{1}) (a_{3} - a_{1})$
or $(\frac{b_{2} - b_{1}}{a_{2} - a_{1}}) (\frac{b_{3} - b_{1}}{a_{3} - a_{1}}) = - 1$
or $(slope of AB) \times (slope of AC) = - 1$
Therefore, the triangle is right -angled at point $(a_{1}, b_{2})$ . Hence, the circumcenter is the midpoint of $(a_{2} b_{2})$ and $(a_{3}, b_{3})$ which is $(\frac{a_{2} + a_{3}}{2}, \frac{b_{2} + b_{3}}{2})$

Updated on:21/07/2023

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE-COORDINATE SYSYEM -JEE Main Previous Year

Home
Ask Doubt
Profile