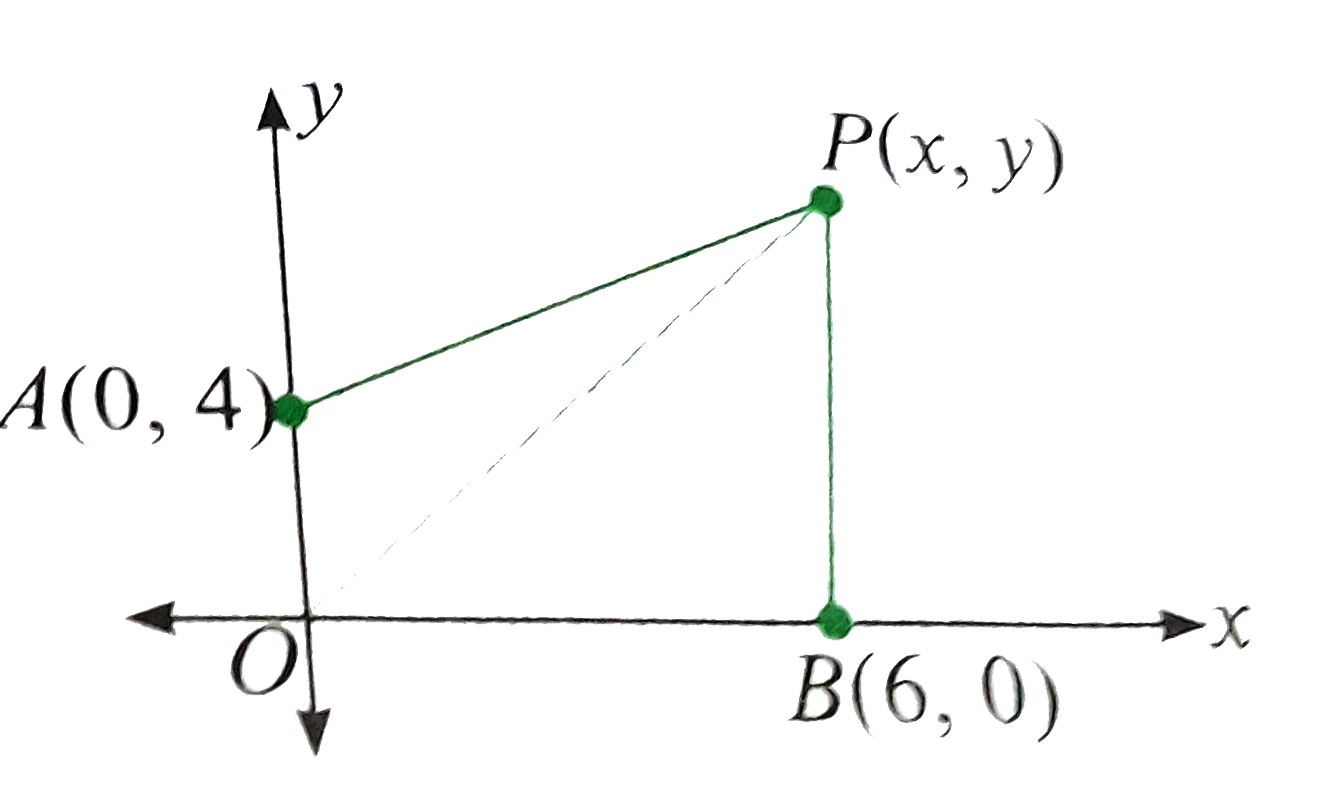
Let 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be x+3y=0 (b) x+2y=0 2x−3y=0 (d) 3y−x=0Solution in Tamil
x+3y=0
x+2y=0
2x−3y=0
3y−x=0
The correct Answer is:A, D
Let point P be (x,y).
arΔPOA=12(OA)|x|=2|x|
arΔPOA=12(OB)|y|=3|y|
∴2|x|=6|y|
or |x|=3|y| or 3y−x=0or3y+x0
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)10videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Matrix)4videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Single)59videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Study the diagram. The line l is perpendicular to line m Does PE bisect CG?
01:47View SolutionConsider the triangle whose vertices are (-1,0),(5,-2) and (8,2). Find the centroid of the triangle.
05:31View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A can be (a)(1,6) (b) (−12,5) (c)(56,6) (d) none of these
04:04View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
06:15View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
03:50View SolutionLet 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
04:59View SolutionThe coordinates of three points O, A, B are (0, 0), (0,4) and (6, 0) respectively. A point P moves so that the area of ΔPOA is always twice the area of ΔPOB. Find the equation to both parts of the locus of P.
03:47View SolutionGiven A(6,0) and B(0,4) and O is the origin.If the locus P such that area of ΔPOB=2 (area of ΔPOA ) is x2−ky2=0 ,then k is equal to
09:03View SolutionThe sides of a triangle are 3x+2y−6=0,2x−3y+6=0,x+2y+2=0. P(0,b) is a point on y-axis. If P lies on the triangle or inside the triangle then the range of b is
07:09View SolutionLet O be the origin and A, B be the two points having coordinates (0, 4) and (6, 0) respectively. If a point P moves in such a way that the area of the ΔOPA is always twice the area of ΔPOB, then P lies on
05:24View SolutionLet O≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
12:17View SolutionLet 0≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be x+3y=0 (b) x+2y=0 2x−3y=0 (d) 3y−x=0
03:11View SolutionLet P and Q be any two points on the lines represented by 2x−3y=0 and 2x+3y=0 respectively. If the area of triangle OPQ (where O is origin) is 5, then which of the following is not the possible equation of the locus of mid-point of PO?
04:02View SolutionThe area of the triangle formed by the lines x + y - 3 = 0, x - 3y + 9 = 0 and 3x - 2y + 1 = 0 is -
04:19View SolutionO(0,0),A(4,0),B(0,6) are the points. If P is a point such that the area of ΔPOB is twice the area of ΔPOA, then the locus of P is
09:01View SolutionThe lines 2x + 3y-1 = 0, x + 2y-1 = 0 and ax + by -1 = 0 form a triangle whose perpendicular point is, then the value of (a, b) is
02:55View Solution

