Consider the parabola (x−1)2+(y−2)2=(12x−5y+3)2169 and match the following lists :

The correct Answer is:a→r;b→s;c→p;d→q.
a→r,b→s,c→p,d→q.
The locus of the point of intersection of perpendicular tangent is directrix, which is 12x-5y+3=0.
The parabola is symmetrical about its axis, which is a line passing through the focus (1,2) and perpendicular to the directrix. So, it has equation 5x+12y-29=0.
The minimum length of focal chord occurs along the latus rectum line, which is a line passing through the focus and parallel to the directrix, i.e., 12x-5y-2=0.
The locus of the foot of perpendicular from the focus upon any tangent is tangent at the vertex, which is parallel to directrix and equidistant from the directrix and latus rectum line.
Let the equation of tangent at vertex be
12x−5y+λ=0
where |λ−3|√122+52=|λ+2|√122+52orλ=12
Hence, the equation of tangent at vertex is 24x-10y+1=0.
Topper's Solved these Questions
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Numerical)
28 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - JEE Main Previous Year
8 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Exercise (Comprehension)
41 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank
4 Videos
Similar Questions
Knowledge Check
The length of the latusretum of the parabola 169∣∣(x−1)2+(y−3)2∣∣=(5x−12y+7)2, is
A1413B2813C1213D4813
If the length of the latus rectum rectum of the parabola 169{(x−1)2+(y−3)2}=(5x−12y+17)2 is L then the value of 13L/4 is _________.
View SolutionIf the length of the latus rectum rectum of the parabola 169{(x−1)2+(y−3)2}=(5x−12y+17)2 is L then the value of 13L/4 is _________.
View SolutionIf the length of the latus rectum rectum of the parabola 169{(x−1)2+(y−3)2}=(5x−12y+17)2 is L then the value of 13L4 is _________.
View SolutionConsider the triangle formed by the lines
y+3x+2=0, 3y-2x-5=0, 4y+x-14=0
Match the following lists:

View SolutionConsider the lines given by
L1:x+3y−5=0
L2:3x−ky−1=0
L3:5x+2y−12=0
Match the following lists.
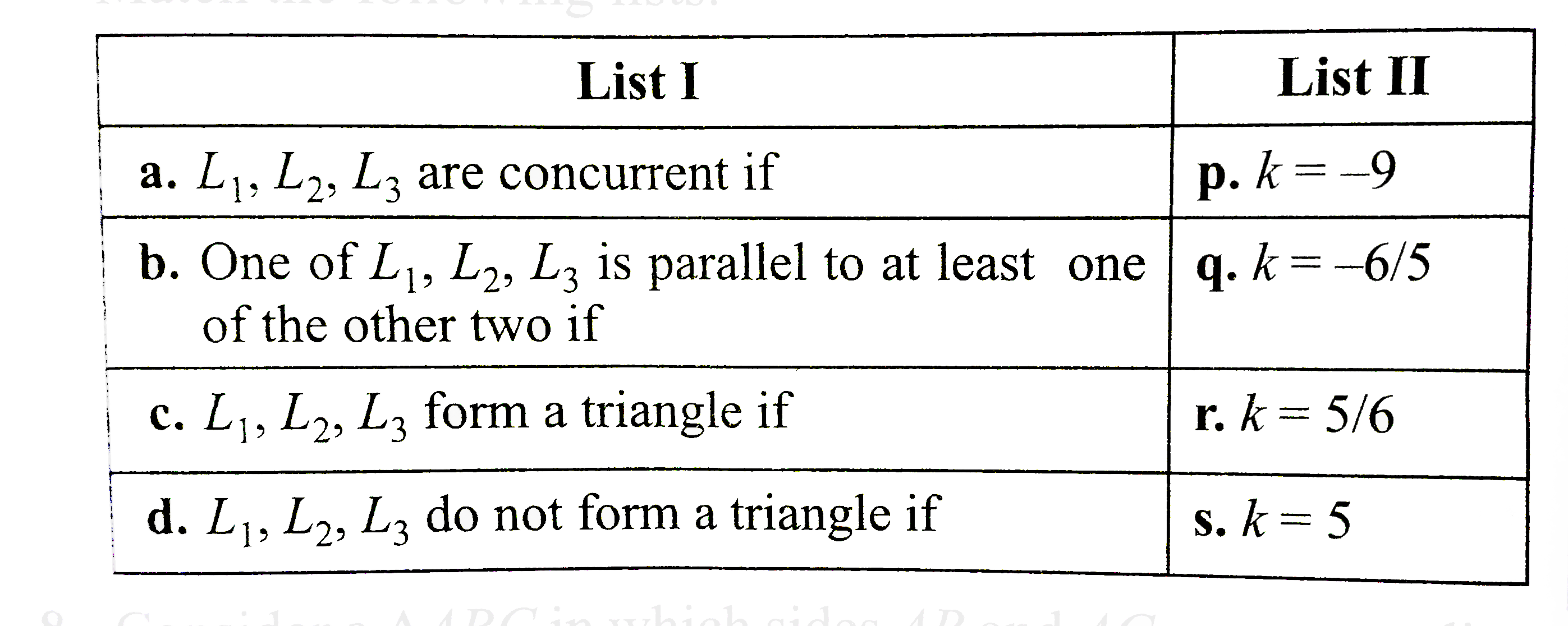
View SolutionConsider the lines given by
L1:x+3y−5=0
L2:3x−ky−1=0
L3:5x+2y−12=0
Match the following lists.
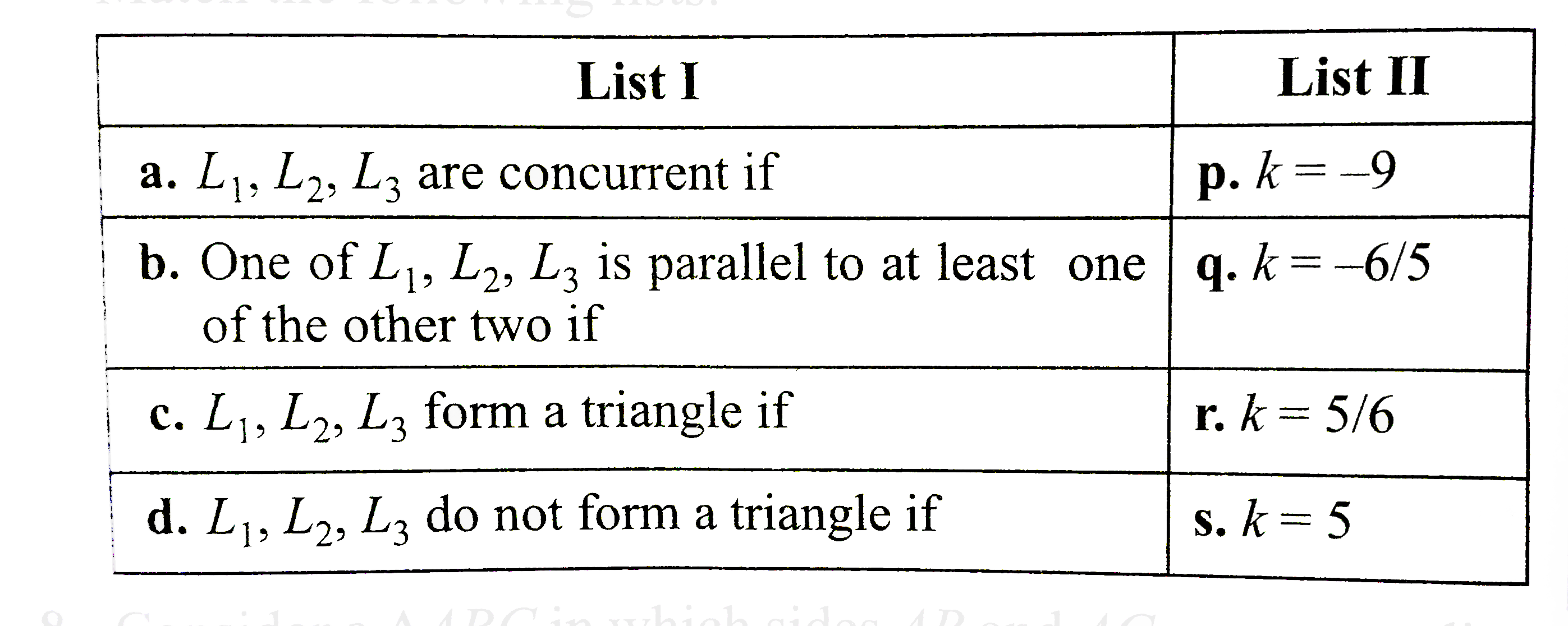
View SolutionConsider the expression 32x2y−12xy2+6x2y2
List out the terms.
View Solution

