Which of the following is the greates? cosec1 (b) cosec2 cosec4 (d) cosec(−6)
cosec 1
cosec 2
cosec 4
cosec (-6)
The correct Answer is:D
(d) Consider sin , sin 2, and -sin6 (sin4 is negative , hence, cosec 4 cancot be maximum).
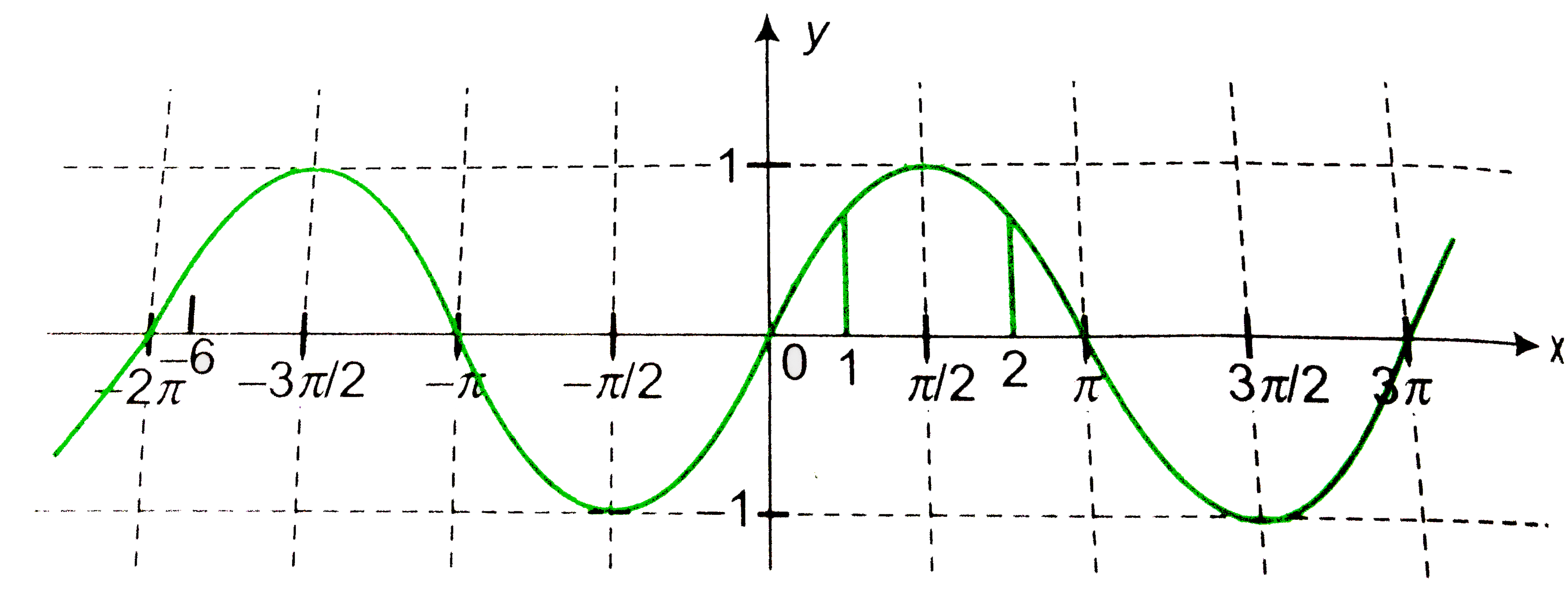 From the graph, sin(-6) is least and positive hence, cosec(-6) is maximum.
From the graph, sin(-6) is least and positive hence, cosec(-6) is maximum.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.18videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.28videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
Prove the following identities: cot4A−1=cosec4A−2cosec2A
View SolutionIn ABC, prove that cosecA2+cosecB2+cosecC2≥6.
View SolutionThe value of cosec100+cosec500−cosec700 is ____
View SolutionIn triangle ABC, prove that cosecA2+cosecB2+cosecC2≥6.
View SolutionProve: cosec Acosec A−1+cosec Acosec A+1=2sec2A
View SolutionFind the number of solution of the equation cos(cos−1x)=cosec(cosec−1x).
View SolutionThe value of √1+cosθ1−cosθ is
(a)cotθ−cosec θ
(b) cosec θ+cotθ
(c) cosec2θ+cot2θ
(d) (cotθ+cosec θ)2View SolutionFind the sum of the series cosecθ+cosec2θ+cosec4θ+→nterms.
View SolutionFind the principal values of each of the following:
(i) cosec−1(−√2)
(ii) cosec−1(−2)View SolutionEvaluate the following integral: ∫π/2π/6cosec xcotx1+cosec2xdx
View Solution

