Minimum value of y=256sin2x+324cosec2x∀x∈R is 432 (b) 504 (c) 576 (d) 776Solution in Tamil
432
504
576
776
The correct Answer is:C
y=256sin2x+324cosec2x
=(16sinx−18cosecx)2+576≥576
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Multiple)
17 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Comprehension)
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.6
9 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
If 0≤θ≤πand81sin2θ+81cos2θ=30 is
View SolutionLet us consider the equation cos4xa+sin4xb=1a+b,x∈[0,π2],a,b>0
The value of sin2x in terms of a and b is
View SolutionProve that: tan7200−cos2700−s∈1500cos1200=14
View SolutionFind the derivative of y=tan−12x3
View SolutionRefer to the following diagram :

Column IColumn IIa.Collinear vectorsp.→ab.Coinitial vectorsq.→bc.Equal vectorsr.→cd.Unlike vectors (same initial point)s.→d
View SolutionMinimum value of y=256sin2x+324cosec2x,∀x∈R is (a) 432 (b) 504 (c) 576 (d) 776
View SolutionThe minimum value of, 25cos e c^2x+16 sin^2x (A) 41 (B) 42 (C) 43 (D) none of these
View SolutionThe minimum value of e2x2−2x+1sin2x is e (b) 1e (c) 1 (d) 0
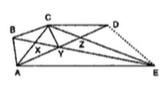
View SolutionIf Figure, CD AE and CYBA Name a triangle equal in area of CBX Prove that ar ( ZDE)= ar ( CZA) Prove that ar (BCZY)=ar ( EDZ)
View Solutionint(sum_(r=0)^(oo)(x^(r)backslash2^(r))/(r!))dx=(A)e^(x)+C(B)(e^(2x))/(2)+C(C)-(2)/(1-2x)+C(D)2e^(2x)+C
View SolutionMinimum value of y=256sin2x+324cosec2x,∀x∈R is (a) 432 (b) 504 (c) 576 (d) 776
View SolutionThe minimum value of e(2x2−2x+1)sin2x is a. e (b) 1e (c) 1 (d) 0
View SolutionIf ∫x2.e−2xdx=e−2x(ax2+bx+c)+d, then the value of ∣∣∣abc∣∣∣ is______
View SolutionIf a,b,c,d∈R+−{1}, then the minimum value of logda+logcb+logac+logbd is
View SolutionIn ABC , AD and BE are altitudes. Prove that ar(DEC)ar(ABC)=DC2AC2
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)=
View Solution
