Solve, $\sqrt{x - 6} - \sqrt{10 - x} \geq 1$ .Solution in Tamil

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $x \in [(16 + \sqrt{7}) / 2, 10]$

We have $\sqrt{x - 6} - \sqrt{10 - x} \geq 1$
We must have $x \geq 6$ and $x \leq 10$
Then $\sqrt{x - 6} \geq 1 + \sqrt{10 - x}$
Squaring given inequality,
$x - 6 \geq 1 + 10 - x + 2 \sqrt{10 - x}$
$\Rightarrow 2 x - 17 \geq 2 \sqrt{10 - x}$
Clearly LHS must be positive.
$∴ x \geq \frac{17}{2}$
So we have
$4 x^{2} + 289 - 68 x \geq 4 (10 - x)$
$\Rightarrow 4 x^{2} - 64 x + 249 \geq 0$
$\Rightarrow x^{2} - 16 x + \frac{249}{4} \geq 0$
$\Rightarrow {(x - 8)}^{2} - {(\frac{\sqrt{7}}{2})}^{2} \geq 0$
$\Rightarrow (x - 8 - \frac{\sqrt{7}}{2}) (x - 8 + \frac{\sqrt{7}}{2}) \geq 0$

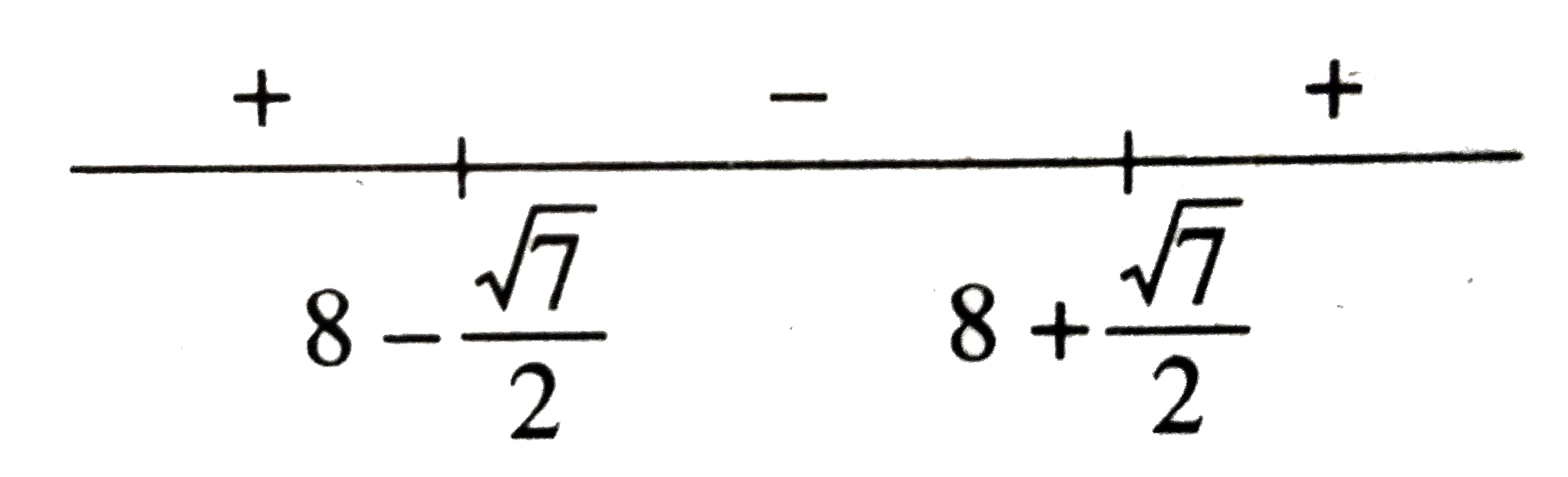
From the sign scheme, $x \in [(16 + \sqrt{7}) / 2, 10]$

|

Updated on:21/07/2023

Class 12 MATHS INEQUALITIES AND MODULUS

Topper's Solved these Questions

Similar Questions

CENGAGE-INEQUALITIES AND MODULUS-Single correct Answer

Home
Ask Doubt
Profile