x3+5x2+px+q=0 and x3+7x2+px+r=0 have two roos in common. If their third roots are γ1 and γ2 , respectively, then |γ1−γ2|=Solution in Tamil
10
12
13
42
The correct Answer is:B
(b) Let the roots of x3+5x2+px+q=0 are α1, β1, γ1……..(i)
Then roots of the x3+7x2+px+r=0 is α1, β1, γ2……..(ii)
From (i)-(ii), −2x2+q−r=0
This equation has roots α1, β1
⇒α1+β1=0
Now from (i)α1+β1+γ1=−5⇒γ1=−5
From (ii)α1+β1+γ2=−7⇒γ2=−7
∴γ1+γ2=−12
∴|γ1+γ2|=12
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Comprehension12videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer6videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank12videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
p(x) be a polynomial of degree at most 5 which leaves remainder - 1 and 1 upon division by (x−1)3 and (x+1)3respectively, the number of real roots of P(x)=0 is
03:33View SolutionIf c≠0 and the equation p/(2x)=a/(x+c)+b/(x−c) has two equal roots, then p can be (√a−√b)2 b. (√a+√b)2 c. a+b d. a−b
01:30View Solutionabout to only mathematics
02:29View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
06:36View Solutionx^(3)+5x^(2)+px+q=0 and x^(3)+7x^(2)+px+r=0 have two roots in common.If their third roots are gamma_(1) and gamma_(2) respectively,then | gamma_(1)+gamma_(2)|=
03:23View SolutionThe coefficient of real expansion of liquid is gamma_(R) and the coefficient of appareent expansion of the liquid is gamma_(A) . The coefficient of cubical expansion of the vessel is gamma . If gamma_(R) : gamma_(A) = 4:1 then gamma_(A) : gamma is
06:05View SolutionOrder of no. of revolutions/sec gamma_(1),gamma_(2),gamma_(3) and gamma_(4) for I, II, III and IV orbits is:
06:05View Solutionx3+5x2+px+q=0 and x3+7x2+px+r=0 have two roos in common. If their third roots are γ1 and γ2 , respectively, then |γ1−γ2|=
View SolutionIF the equations x3+5x2+px+q=0andx3+7x2+px+r=0 have two roots in common, then the product of two non-common roots of two equations, is
03:39View SolutionLet α,β,γ be the roots of x3+x+10=0 and α1=α+βγ2,β1=β+γα2,γ1=γ+αβ2. Then, the value of (α31+β31+γ31)−110(α21+β21+γ21) is
03:28View SolutionLet α,β,γ be the roots of x3+x+10=0 and α1=α+βγ2,β1=β+γα2,γ1=γ+αβ2. Then, the value of (α31+β31+γ31)−110(α21+β21+γ21) is
View SolutionLet α,β,γ be the roots of x3+x+10=0. Write α1=α+βα2,β1=β+γα2,γ1=γ+αβ2. Then the value of (α31+β31+γ31)−110(α21+β21+γ21) is
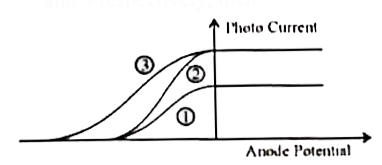
01:36View SolutionThe following graph represents the variation of photo current with anode potential for a metal surface . Here l1,l2 and l3 represents intensities and γ1,γ2, γ3 respectively , them .
 07:13View Solution
07:13View Solutionx3+5x2+px+q=0 and x3+7x2+px+r=0 have two roos in common. If their third roots are γ1 and γ2 , respectively, then |γ1+γ2|=
07:25View SolutionγA of liquid is 7/8 of γR of liquid. αgof vessel is
03:41View Solution

