If the quadratic equation x2−36x+λ=0 has roots α and β such that α, β∈N and (lambda)/(5) cancel in Z and λ assumes minimum possible value then √α+2√β+2|α−β| is equal toSolution in Tamil
38
316
√11134
√11117
The correct Answer is:A
(a) x2−36x+λ=0
∴Λ=36x−x2
α=1, λ=5, β=35 (rejected)
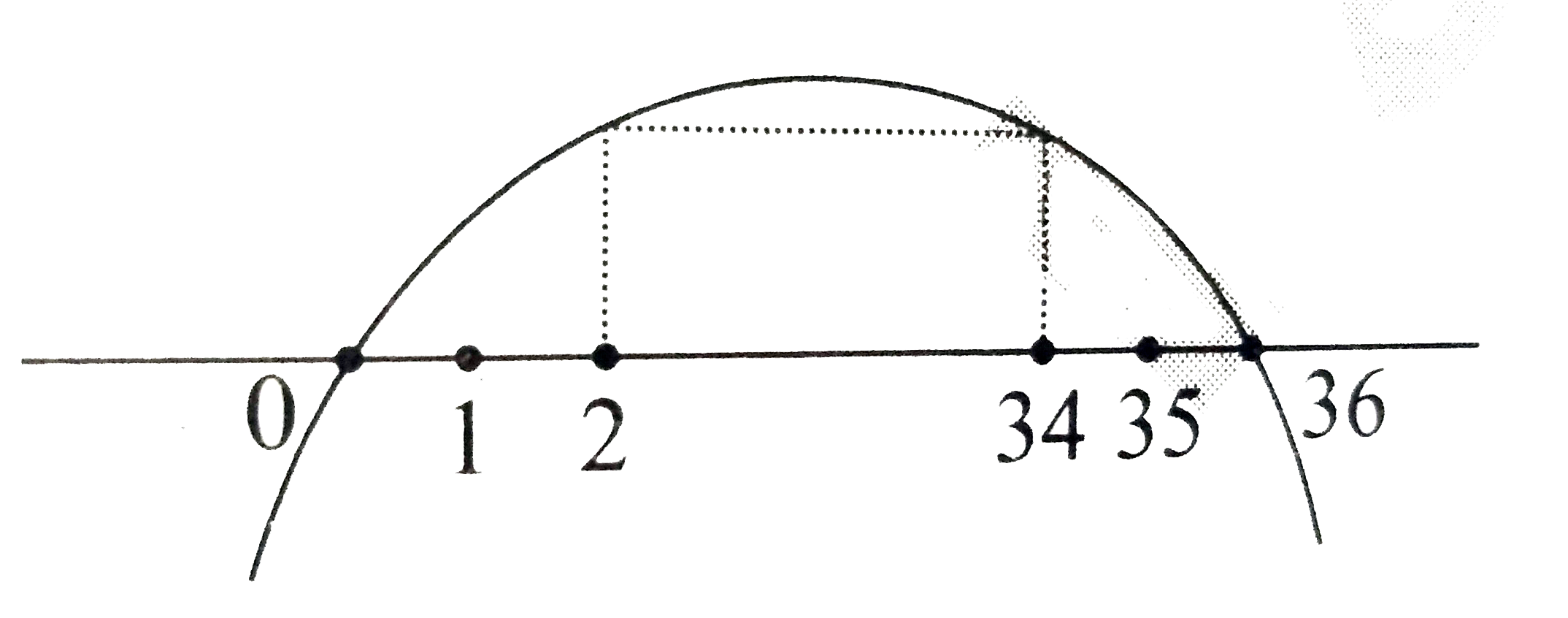
∴α=2, λ=68, β=34 or α=34, β=2
∴√36√432=38
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Comprehension12videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer6videos
THEORY OF EQUATIONS
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year4videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank12videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
p(x) be a polynomial of degree at most 5 which leaves remainder - 1 and 1 upon division by (x−1)3 and (x+1)3respectively, the number of real roots of P(x)=0 is
02:11View SolutionIf c≠0 and the equation p/(2x)=a/(x+c)+b/(x−c) has two equal roots, then p can be (√a−√b)2 b. (√a+√b)2 c. a+b d. a−b
01:23View Solutionabout to only mathematics
02:16View SolutionThe equation of the plane which has the property that the point Q(5,4,5) is the reflection of point P(1,2,3) through that plane, is ax+by+cz=d where a,b,c,d∈N. Find the least value of (a+b+c+d).
02:24View SolutionIf alpha,beta be the roots of 4x^(2)-17x+lambda=0,lambda in R such that 1
01:18View SolutionIf alpha and beta are the roots of the equation x^(2)+sqrt(alpha)x+beta=0 then the values of alpha and beta are.-
00:49View SolutionIf alpha and beta are the roots of the equation x^(2)+sqrt(alpha)x+beta=0 then the values of alpha and beta are
01:45View SolutionIf (cosα+cosβ)2+(sinα+sinβ)2=λcos2(α−β2), write the value of λ.
04:06View SolutionIf alpha, beta are the roots of x^2 – 3x + lambda = 0 (lambda in R) and alpha < 1
02:09View SolutionIf alpha and beta are the roots of the equation x^(2)+6x+lambda=0 and 3 alpha+2 beta=-20 ,then lambda=
07:25View SolutionIf the quadratic equation x2−36x+λ=0 has roots α and β such that α, β∈N and (lambda)/(5) cancel in Z and λ assumes minimum possible value then √α+2√β+2|α−β| is equal to
08:42View SolutionLet α,β be the roots of x2+(3−λ)x−λ=0, then the value of λ for which α2+β2 is minimum, is-
04:24View SolutionIf α,β are the roots of the equation :
x2+x√α+β=0, then the values of αandβ are :04:15View Solutionalpha , beta are the roots of the equation lambda (x^(2) - x) + x + 5 = 0 . If lambda_(1) and lambda_(2) are the two values of lambda for which the roots alpha , beta are connected by the relation (alpha)/(beta) + (beta)/(alpha) = 4. Then the value of (lambda_(1))/(lambda_(2)) + (lambda_(2))/(lambda_(1)) is :
01:17View Solutionसिद्ध कीजिए कि :
∣∣ ∣ ∣∣αβλα2β2λ2(β+λ)(λ+α)(α+β)∣∣ ∣ ∣∣=(α−β)(β−λ)(λ−α)(α+β+λ)01:21View SolutionIf roots α,β of the equation x2−bxax−c=λ−1λ+1 are such that α+β=0, then the value of λ is
07:17View Solution

