Question

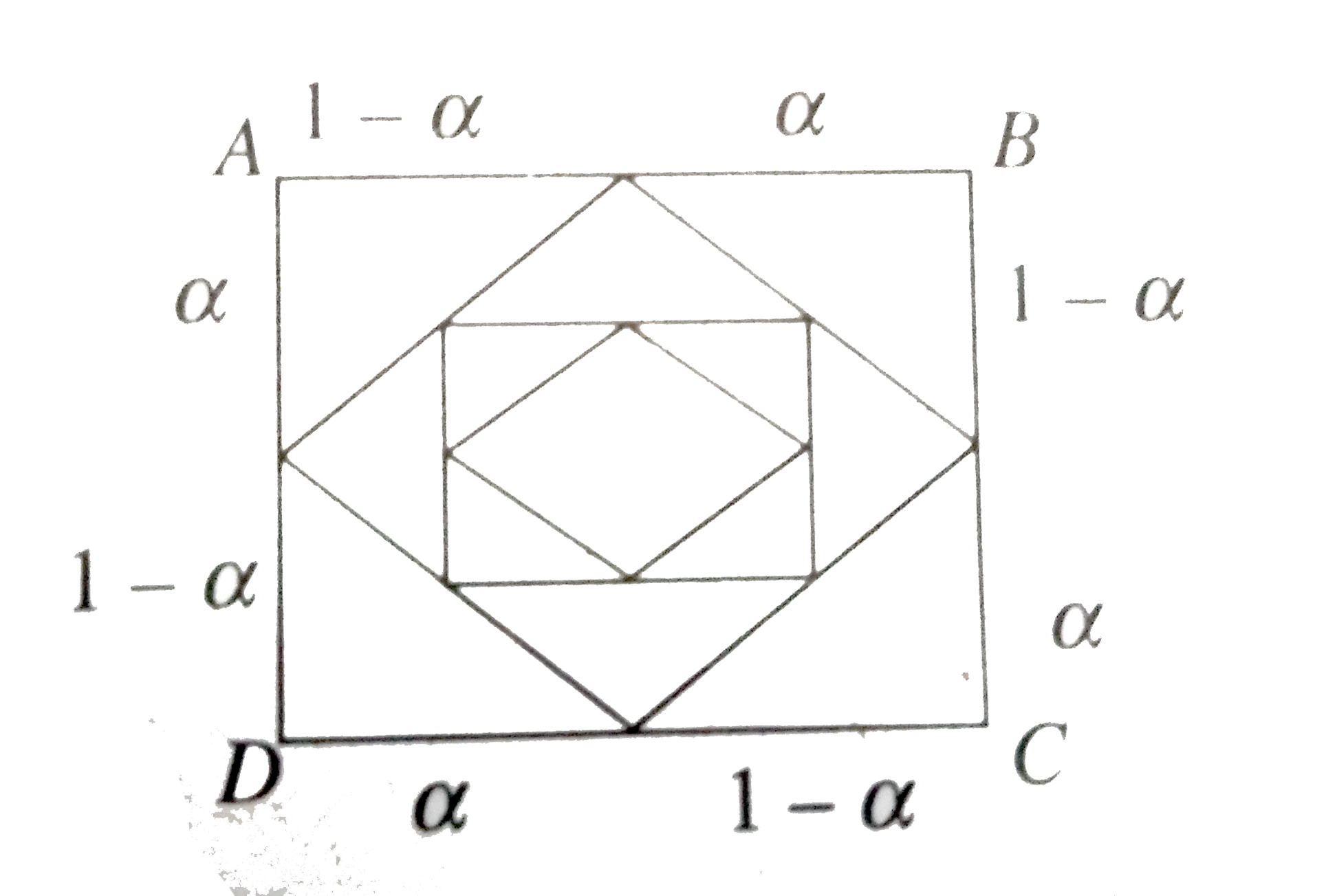
Let $ABCD$ is a unit square and each side of the square is divided in the ratio $\alpha :(1-\alpha )(0<\alpha <1)$ . These points are connected to obtain another square. The sides of new square are divided in the ratio $\alpha :(1-\alpha )$ and points are joined to obtain another square. The process is continued idefinitely. Let $a_n$ denote the length of side and $A_n$ the area of the $n^{th}$ square
The value of $\alpha$ for which $\sum _{n=1}^{\infty }{A}_n=\frac{8}{3}$ is/are

Options

A. `(1)/(3)`, `(2)/(3)`
B. `(1)/(4)`, `(3)/(4)`
C. `(1)/(5)`, `(4)/(5)`
D. `(1)/(2)`

Answer

B

Explanation

`(b)`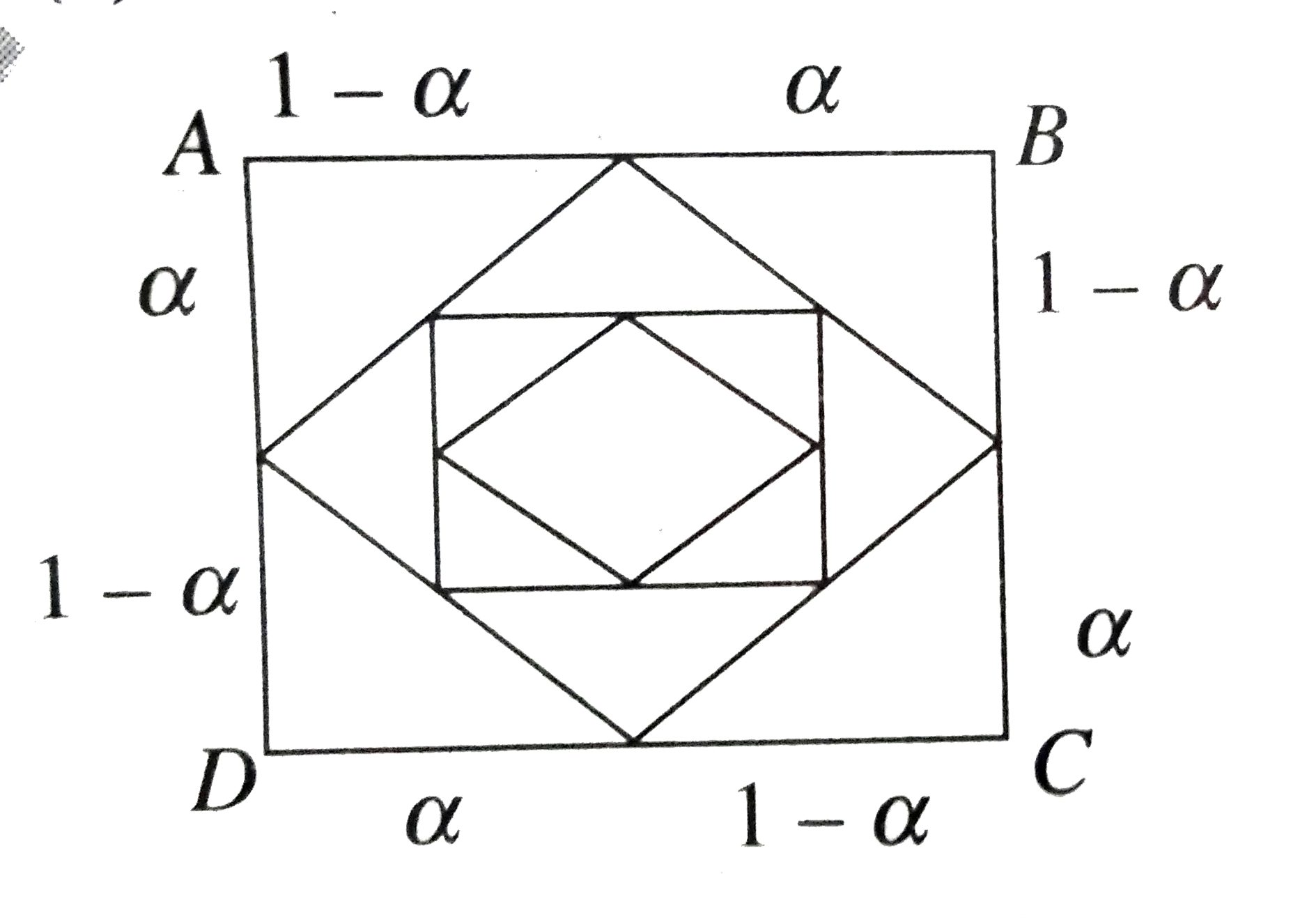
Clearly from the diagram,
`a_(1)=1`
`(a_(n+1))^(2)=[(1-alpha)^(2)+alpha^(2)](a_(n))^(2)impliesA_(n+1)=[2alpha^(2)-2alpha+1]A_(n)`
For `alpha=(1)/(3)`, `(a_(n+1))^(2)=(5)/(9)(a_(n))^(2)`
`implies(A_(n+1))/(A_(n))=(5)/(9)`
`impliesA_(2)=(5)/(9)`, `A_(3)=((5)/(9))^(2)`,...
`impliesA_(n)=((5)/(9))^(n-1)`
`A_(n) lt (1)/(10) implies ((5)/(9))^(n-1) lt (1)/(10)`
`implies` Least value of `n` is `5`.
`sum_(n=1)^(oo)A_(n)=(8)/(3)`
`implies(1)/(1-(2alpha^(2)-2alpha+1))=(8)/(3)`
`implies16alpha^(2)-16alpha+3=0`
`implies16alpha^(2)-12alpha-4alpha+3=0`
`implies(4alpha-1)(4alpha-3)=0`
`impliesalpha=(1)/(4)`, `(3)/(4)`
The side of `n^(th)` square equal to the diagonal of `(n+1)^(th)` square. ,brgt `impliessqrt(2)a_(n)=a_(n+1)`
`implies((a_(n+1))^(2))/((a_(n))^(2))=(1)/(2)`
`implies4alpha^(2)-4alpha+1=0`
`impliesalpha=1//2`