How many six-digit numbers are there in which no digit is repeated, even digits appear at even places, odd digits appear at odd places and the number is divisible by 4 ?
A
3600
B
2700
C
2160
D
1440
Text Solution
The correct Answer is:D
(d) The number formed by last two digits must be divisible by 4.
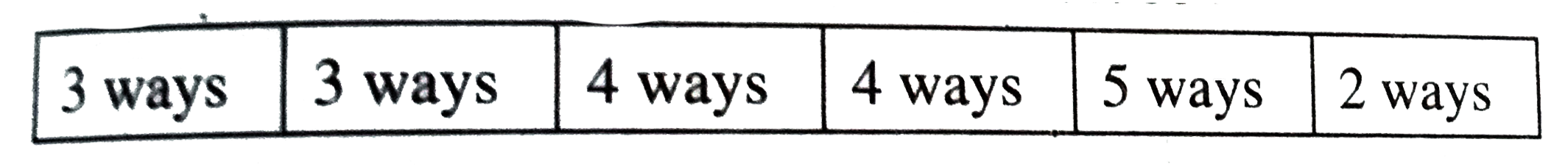
3×3×4×4×5×2=1440
|
Topper's Solved these Questions
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Multiple Correct Answer
2 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Question Bank
9 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - CENGAGECHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise
9 Videos
Similar Questions
Knowledge Check
How many 4-digit numbers are there with no digit repeated?
A=9⋅9⋅8⋅7B=10⋅9⋅8⋅7C=9⋅8⋅7DNone of theseHow many three digit numbers are there in which all the digits are odd?
A100B125C500D250How many 6-digit numbers have all their digits either all odd or all even?
A31250B28125C15625DNone of these
How many 3 digit numbers are there, with distinct digits, with each digit odd?
View SolutionHow many 3 digit numbers are there, with distinct digits, with each digit odd?
View SolutionTotal number of 6-digit numbers in which all the odd digits appear, is
View SolutionIn a six digit number, the sum of the digits in the even places is 9 and the sum of the digits in the odd places is 20. All such numbers are divisible by
View SolutionTotal number of 6-digit numbers in which all the odd digits appear, is
View Solution
