Let A={x:−1≤x≤1}=B be a function f:A→B. Then find the nature of each of the following functions.
(i) f(x)=|x| (ii) f(x)=x|x|
(iii) f(x)=x3 (iv) f(x)=sinπx2
Text Solution
(i) f:[−1,1]→[−1,1], where f(x)=|x|.
Graph of the function is as shown in the following figure.
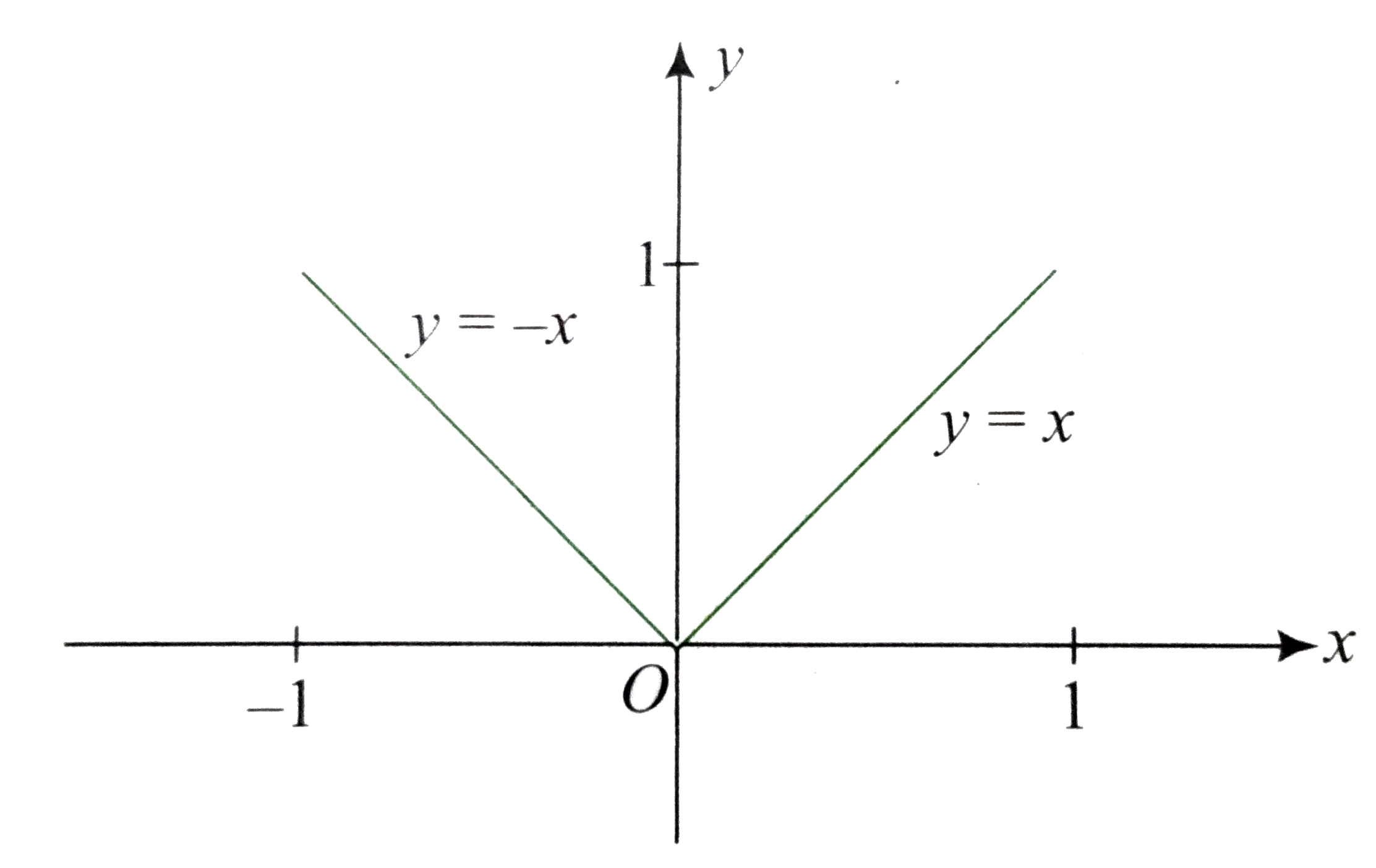
From the graph we observe that f(x) is many-one.
Also, we observe that the range is [0,1]. Hence f(x) is into.
(ii) f:[−1,1]→[−1,1], where f(x)=x|x|
Now f(x)=x|x|={x×x, x≥0x×(−x), x<0={x2, x≥0−x2, x<0
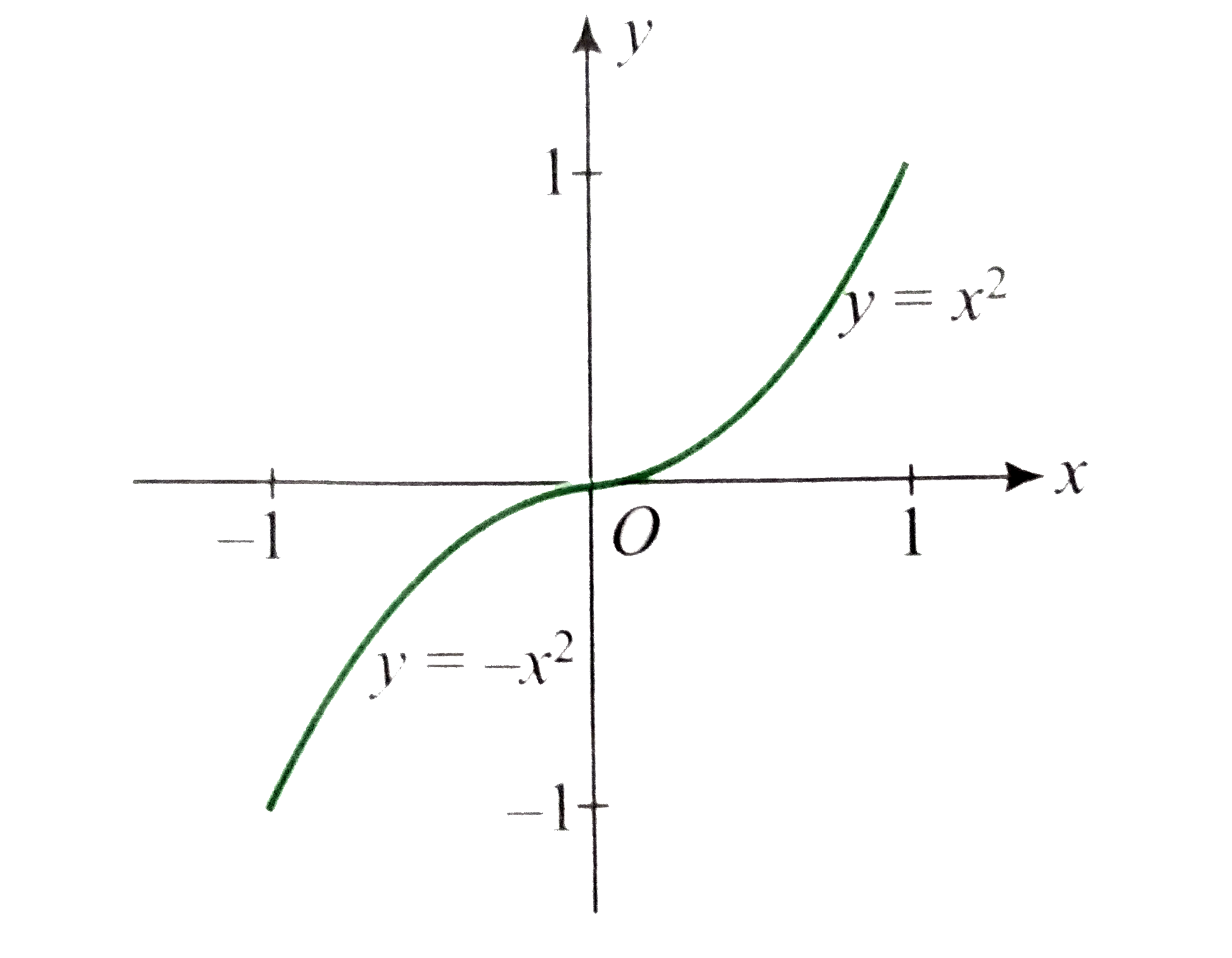
From the graph we observe that f(x) is one-one as there is no horizontal line which intersect the curve more than once.
Also, we observe that the range is [−1,1]. Hence f(x) is onto.
Thus f(x) is bijective.
(iii) f:[−1,1]→[−1,1], where f(x)=x3

Clearly, f(x) is one-one.
Also, for x∈[−1,1],x3∈[−1,1].
So, f(x) is onto.
Thus, f(x) is bijective.
(iv) f:[−1,1]→[−1,1], where f(x)=sinπx2
For x∈[−1,1],πx2∈[−π2,π2]
So, graph of f(x) is as shown in the following figure.
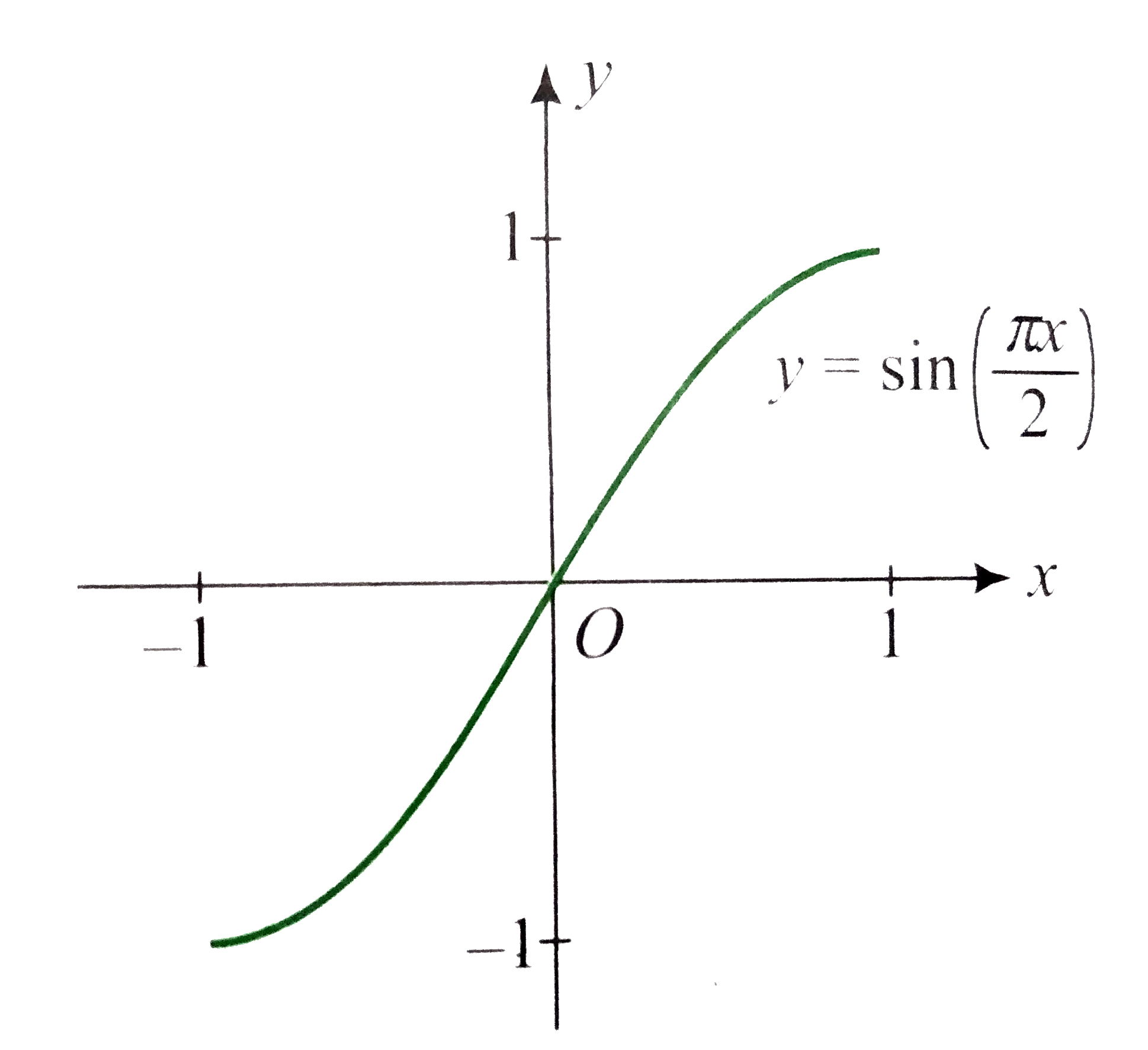
From the graph we observe that f(x) is one-one.
Also, range of the f(x) is [−1,1]. Hence f(x) is onto.
Thus, f(x) is bijective.
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.1
15 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.2
5 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year
12 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Knowledge Check
The function f(x)=cosx,0≤x≤π is
AdecreasingBincreasingCneither increasing nor decreasingDincreasing for 0≤x≤πLet A={−1≤x≤1}andf:A→A such that f(x)=x|x| then f is:
Aa bijectionBinjective but not surjectiveCsurjective but not injectiveDneither injective nor surjective
Find the range of the following functions
(i) f(x)=log2(√x−4+√6−x),4≤x≤6
(ii) f(x)=9x−3x+1
View SolutionFind the range of the following functions
(i) f(x)=log2(√x−4+√6−x),4≤x≤6
(ii) f(x)=9x−3x+1
View SolutionLet A={x−1≤x≤1}andf:A→A such that f(x)=x|x| then f is:
View SolutionIf f(x) is a real valued function, then which of the following is injective function ?
(i) f(x)=x5 (ii) f(x)=x+sinx
(iii) f(x)=x2 (iv) f(x)=ex
(v) f(x)=x3+x2+4x+4
View SolutionIf f(x) is a real valued function, then which of the following is injective function ?
(i) f(x)=x5 (ii) f(x)=x+sinx
(iii) f(x)=x2 (iv) f(x)=ex
(v) f(x)=x3+x2+4x+4
View SolutionLet A={−1≤x≤1}andf:A→A such that f(x)=x|x| then f is:
View Solution
