Match the following lists and then choose the correct code.

A
abcdqsrp
B
abcdpsrs
C
abcdqsps
D
abcdspqr
Text Solution
The correct Answer is:C
p. y=tanx=1x2
From the graph, it is clear it will have two real roots.
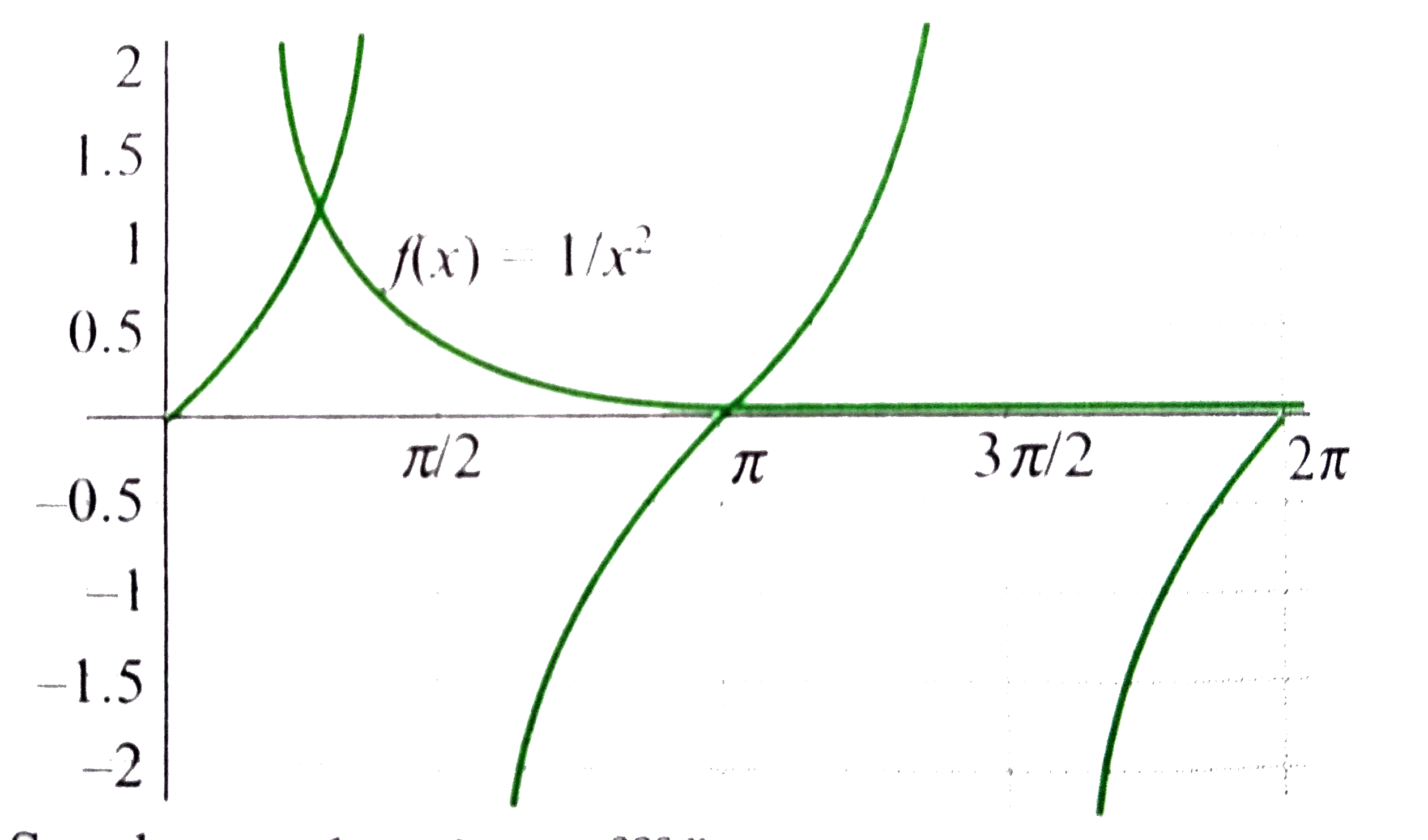
q. See the graphs of y=2cosxandy=|sinx|. Two curves meet at four points for x∈[0,2π].

So, the equation 2cosx=|sinx| has four solutions.
r. Given that f(|x|)−0 has 8 real roots or f(x)=0 has four positive roots.
Since f(x) is a polynomial of degree 5,f(x) cannot have even number of real roots.
Hence, f(x) has all the five roots real and one root is negative.
s. 7|x|(|5−|x∣)=1.
or|5−|x∣∣=7−|x|
Draw the graph of y=7−|x|andy=|5−|x∣∣.
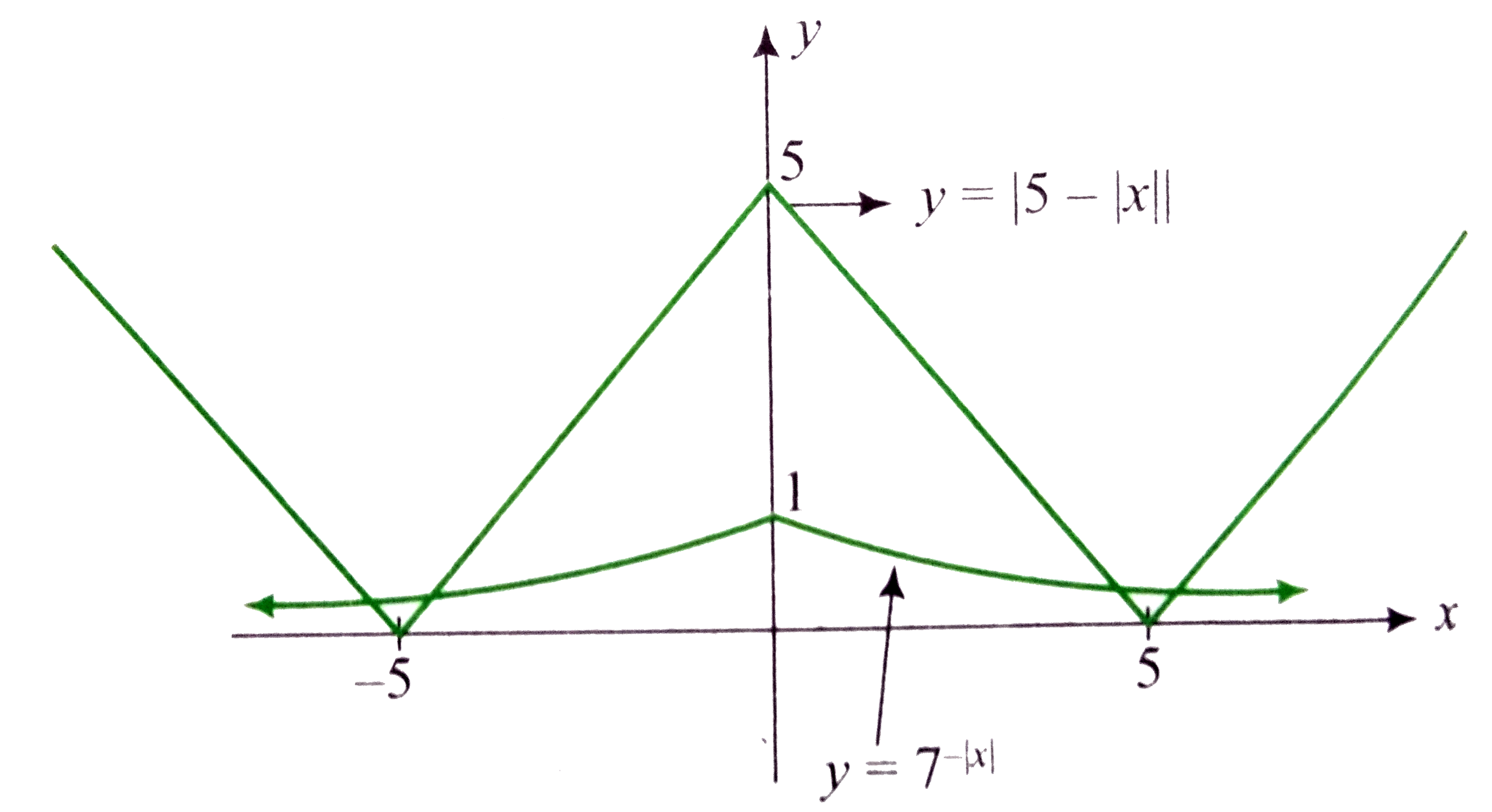
From the graph, the number of roots is 4.
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Numerical)
31 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year
12 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Knowledge Check
Match the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqpMatch the following two lists and choose the correct answer from the codes given below:
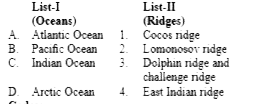 AA-2,B-4,C-1,D-3BA-3,B-1,C-4,D-2CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1
AA-2,B-4,C-1,D-3BA-3,B-1,C-4,D-2CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1Match the following two lists and choose the correct answer from the codes given below:
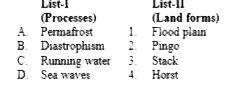 AA-2,B-4,C-1,D-3BA-2,B-1,C-4,D-3CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1
AA-2,B-4,C-1,D-3BA-2,B-1,C-4,D-3CA-1,B-2,C-3,D-4DA-4,B-3,C-2,D-1
Match the following columns and choose the correct code.

View SolutionList ‘A’ consists of the dynasties and List ‘B’ consists of their capital cities. Match the lists and choose the correct answer from the codes given below :

View SolutionMatch the following column and choose the correct code
View SolutionMatch the relation for derivatives given in List II with the relation given in List I and then choose the correct code.

View SolutionMatch List I with List II and choose the correct code
View Solution


