Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2andf(5)=4∈[−5,5], then the minimum number of roots of the equation f(x)=0 isSolution in Tamil
The correct Answer is:3
f(x)+f(−x)=0
Therefore,f(x) is an odd function.
Since points (-3, 2) and (5, 4) lie on the curve,
∴ (3, -2) and (-5, -4) will also lie on the curve.
For minimum number of roots, graph of continuous function f(x) is as follows:
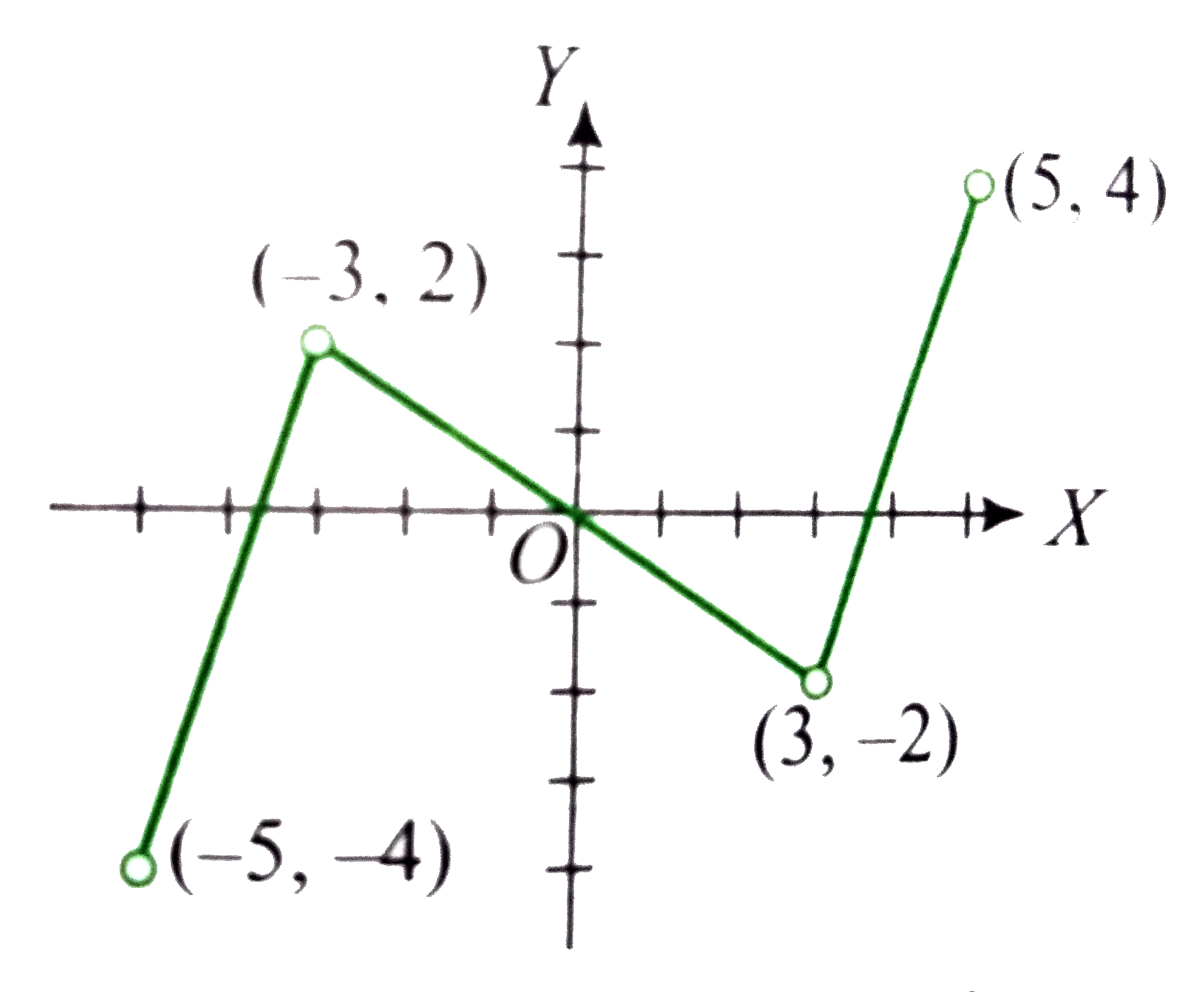
From the above graph of f(x), it is clear that equation f(x)=0 has at least three real roots.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year
12 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
For real x, let f(x)=x3+5x+1 , then (1) f is oneone but not onto R (2) f is onto R but not oneone (3) f is oneone and onto R (4) f is neither oneone nor onto R
View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
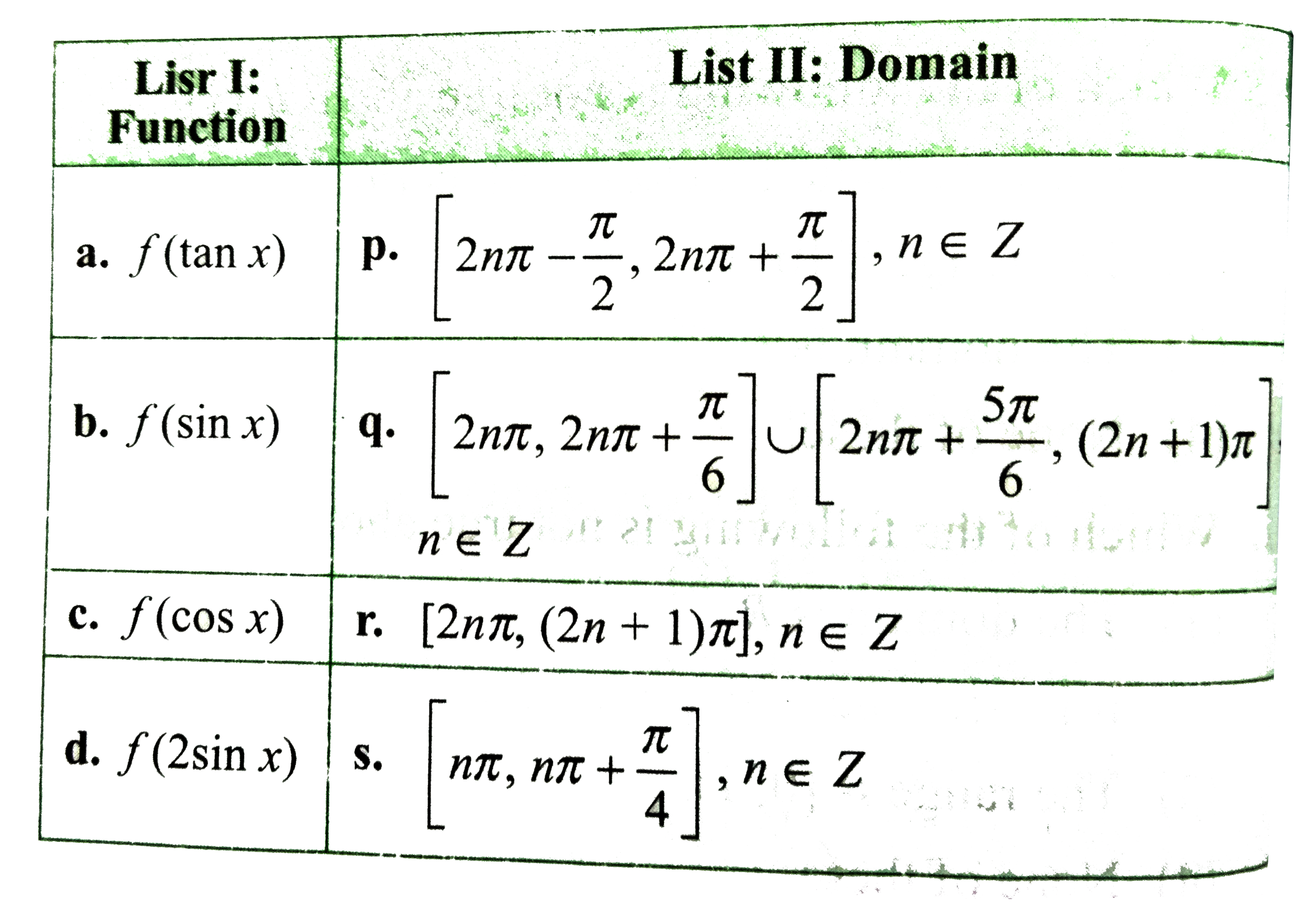
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2andf(5)=4∈[−5,5], then the minimum number of roots of the equation f(x)=0 is
View SolutionLet f:R rarr R be a continuous onto function satisfying f(x)+f(-x)=0AA x in R, If f(-3)=2 and f(5)=4 in [-5,5], then the equation f(x)=0 has
View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0,∀x∈R . If f(−3)=2andf(5)=4 in [-5, 5], then what is the minimum number of roots of the equation f(x) = 0?
View SolutionLet a function f:R→R, where R is the set of real nos. satisfying the equation f(x+y)=f(x)+f(y)∀x,y if f(x) is continuous at x = 0, then
View SolutionLet f(x) be a continuous & differentiable function on R satisfying f(−x)=f(x)&f(3+x)=f(3−x)∀x∈R. If f'(1)=−5 then f'(7) =
View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2 and f(5)=4 in [−5,5], then the minimum number of roots of the equation f(x)=0 is
View SolutionLet f(x) be continuous functions f:R→R satisfying f(0)=1andf(2x)−f(x)=x. Then the value of f(3) is 2 b. 3 c. 4 d. 5
View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0,∀x∈R . If f(−3)=2andf(5)=4 in [-5, 5], then what is the minimum number of roots of the equation f(x) = 0?
View SolutionLet f(x) be continuous functions f:R→R satisfying f(0)=1andf(2x)−f(x)=x. Then the value of f(3) is 2 b. 3 c. 4 d. 5
View SolutionLet a function f: R to R , where R is the set of real nos. satisfying the equation f(x+y) = f(x) + f(y) AA x, y if f(x) is continuous at x = 0, then
View Solutionएक सतत् एवं आच्छादक फलन f:R→R इस प्रकार से है कि f(x)+f(−x)=0,∀x∈R. यदि f(-3)=2 तथा f(5)=4 तो अन्तराल [-5,5], में f(x)=0 का-
View SolutionLet f:R→R be a function satisfying f(2−x)=f(2+x)andf(20−x)=f(x)∀x∈R.For this functions f. answer the following
The graph of y = f(x) is not symmetrical about
View Solution
