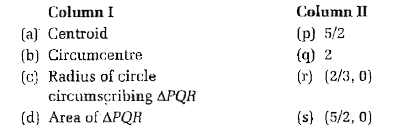Let A,B and C be three distinct points on y2=8x such that normals at these points are concurrent at P. The slope of AB is 2 and abscissa of centroid of ΔABC is 43. Which of the following is (are) correct?
A
Area of ΔABC is 8 sq. units
B
Coordinates of P≡(6,0)
C
Angle between normals are 45∘,45∘,90∘
D
Angle between normals are 30∘,30∘,60∘
Text Solution
The correct Answer is:A, B, C
Let A=(2t21,4t1),B=(2t22,4t2) and C=(2t23,4t3)
Slope of AB=2⇒t1+t2=1 and t1+t2+t3=0 So, t3=−1
Also, 2(t21+t22+t23)3=43⇒t21+t22=1
⇒t1=1,t2=0
A=(2,4),B=(0,0) and C=(2,−4)
Hence P=(6,0)
|
Topper's Solved these Questions
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Comprehension Type
1 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Matching Column Type
1 Videos
- PARABOLABOOK - CENGAGECHAPTER - PARABOLAEXERCISE - Single Correct Answer Type
46 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGECHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Exercise (Numerical)
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGECHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Question Bank
4 Videos
Similar Questions
Knowledge Check
The normals at three points P,Q,R of the parabola y2=4ax meet in (h,k) The centroid of triangle PQR lies on (A)x=0(B)y=0(C)x=-a(D)y=a
Ax = 0By = 0Cx = -aDy = aThe normals at three points P,Q and R of the parabola y2=4ax meet at (h,k). The centroid of the △PQR lies on
Ax=0By=0Cx=-aDy=aIf the three distinct lines
x+2ay+a=0,x+3by+b=0 and
x+4ay+a=0 are concurrent , then the point (a,b) lies on a .AcircleBstraight lineCparabolaDhyperbola
Let P,Q,R be three points on a parabola, normals at which are concurrent, the centroid of ΔPQR must lie on
View SolutionThe equation of the plane, which cuts the coordinate axes at A,B and C such that the centroid of ΔABC is at the point (-2,-1,-4),is
View SolutionIf the three distinct lines
x+2ay+a=0,x+3by+b=0 and
x+4ay+a=0 are concurrent , then the point (a,b) lies on a .
View SolutionLet P , Q and R are three co-normal points on the parabola y2=4ax. Then the correct statement(s) is /at
View SolutionLet P , Q and R are three co-normal points on the parabola y2=4ax. Then the correct statement(s) is /at
View Solution