A point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:Solution in Tamil
a circle
an ellipse
a hyperbola
a pair of lines
The correct Answer is:C, D
Let the two sides of the rectangle lie along x-axis and y-axis.
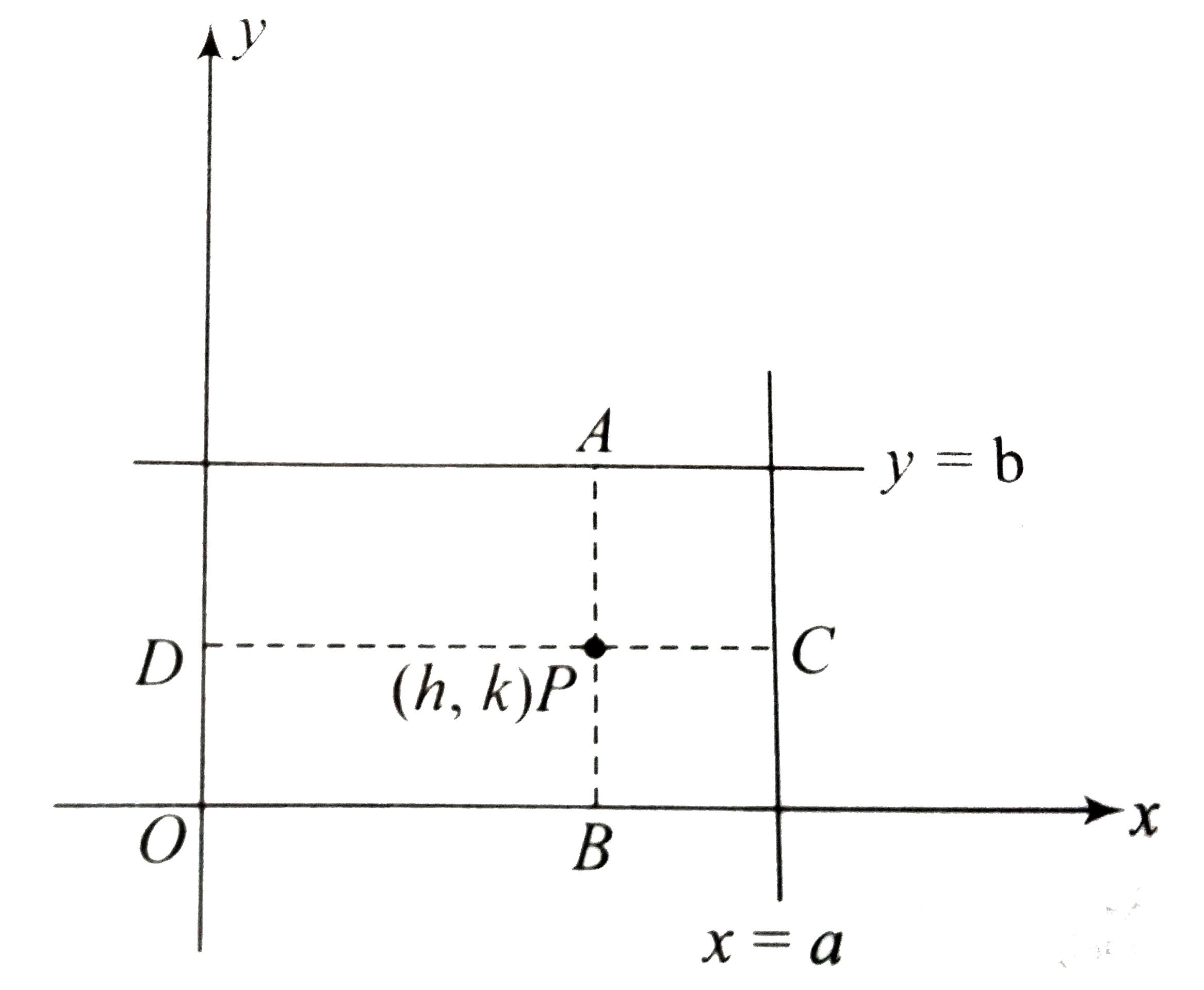
Let point P be (h,k)
Given that
(PA)2+(PB)2=2(PC2+PD2)
⇒k2−(k−b)6(2)=2(h2+(a−h)2)
⇒2k2−2kb+b2=4h2−4ah+2a2
Replacing h by x and k by y
⇒2y2−2by+b2=4x2−4ax+2a2
or 2(y2−by)+b2=4(x2−ax)+2a2
or 4(x−a2)2−2(y−b2)2=b22−a2
Hence it is a hyperbola if b22−a2≠0
or pair of lines if b22−a∘=0
Similar Questions
The point P moves such that the sum of the squares of its distances from two fixed points A(a,0)andB(−a,0) is constant and equal to 6a2. The locus of P is
02:53View SolutionThe locus of a point, which moves in such a way that the sum of the squares of its distances from the four sides of a square is consant (=2c2) is
04:02View Solutionकिसी चर बिंदु की दो स्थिर बिंदुओं से दूरियों के वर्गों का योग एक अचर राशि है । उसके बिन्दुपथ का समीकरण ज्ञात कीजिए ।
09:07View SolutionA point moves so that the sum of squares of its distances from the points (1,2) and (-2,1) is always 6. then its locus is
05:22View SolutionThe sum of the squares of the distances of a moving point from two fixed points (a,0) and (−a,0) is equal to a constant quantity 2c2. Find the equation to its locus.
03:39View SolutionA point moves such that the sum of the squares of its distances from the two sides of length ‘a’ of a rectangle is twice the sum of the squares of its distances from the other two sides of length b. The locus of the point can be:
07:27View Solutionएक बिन्दु इस प्रकार गति करता है कि इसकी एक इकाई लम्बाई भुजा वाले वर्ग की भुजाओं से दूरियों के वर्गों का योग 9 रहता है, तो इस बिन्दु का बिन्दुपथ होगा
05:03View SolutionThe point P moves such that the sum of the squares of its distances from two fixed points A(a,0),B(−a,0) is 8a2 the locus of P is
02:42View Solution

