If the straight line x−2y+1=0 intersects the circle x2+y2=25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x2+y2=25. Solution in Tamil
Let R(h,k) be the point of intersection of the tangents drawn at P and Q to the given circle. Then PQ is the chord of the cord of tangents drawn from R to x2+y2=25
So, its equation is
hx+ky−25=0 (1)
It is given that the eqation of PQ is
x−2y+1=0 (2)
Since (1) and (2) represent the same line, we have
h1=k−2=−251
or h=−25,k=50
Hence, the required point is (−25,50)
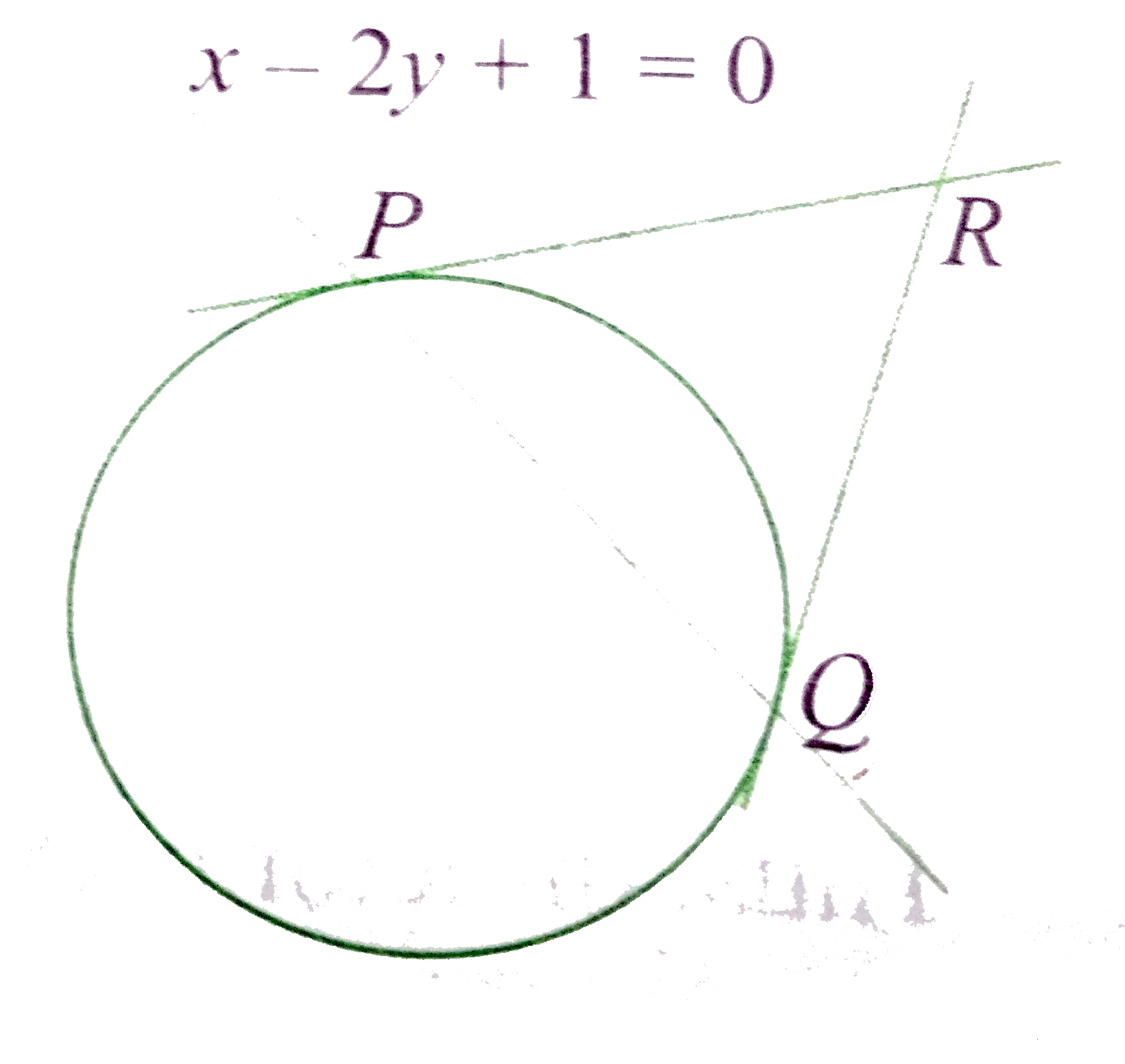
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionIf the straight line x-2y+1=0 intersects the circle x^(2)+y^(2)=25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x^(2)+y^(2)=25
View SolutionIf the line x-y-1=0 intersect the parabola y^(2)=8x at P and Q, then find the point on intersection of tangents P and Q.
View SolutionThe straight line x-2y+1=0 intersects the ci ordinates of a point of intersection of tan circlex x^(2)+y^(2)=25 points T and T' ,find the co- gents drawn at T and T' to the circle.
View SolutionIf 3x+4y=12 intersect the ellipse (x^(2))/(25)+(y^(2))/(16)=1 at P and Q, then point of intersection of tangents at P and Q.
View Solutionif a variable tangent of the circle x^(2)+y^(2)=1 intersects the ellipse x^(2)+2y^(2)=4 at P and Q. then the locus of the points of intersection of the tangents at P and Q is
View SolutionThe straight line x-2y+1=0 intersects the circle x2+y2=25 in points P and Q the coordinates of the point of intersection of tangents drawn at P and Q to the circle is
View SolutionA line through the origin meets the circle x2+y2=a2 at P and the hyperbola x2−y2=a2 at. Q the locus of the point of intersection of the tangents at P to the circle and with the tangents at Q to the hyperbola is
View Solutionx2+y2+6x+6y=2বৃত্তের ওপর P বিন্দুতে অঙ্কিত স্পর্শক 5x−2y+6=0সরলরেখা y-অক্ষের ওপর Q বিন্দুতে ছেদ করলে PQ-এর দৈর্ঘ্য হবে-
View SolutionIf the circle x^(2)+y^(2)=1 A variable tangent of the ellipse x^(2)+2y^(2)=4 Is cut at points P and Q. Then the point of intersection of the tangent lines drawn at P and Q is
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View SolutionIf the straight line x−2y+1=0 intersects the circle x2+y2=25 at points P and Q, then find the coordinates of the point of intersection of the tangents drawn at P and Q to the circle x2+y2=25.
View Solution
