ABC is any triagnel inscribed in the circle $x^{2} + y^{2} = r^{2}$ such that A is fixed point . If the external and internal bisectors of $∠ A$ intersect the circle at D and E, respectively, then which of the following statements is true $Δ A D E$ ?

A

Its centroid is a fixed point.

B

Its circumcentre is a fixed point.

C

Its orthocentre is a fixed point.

D

none of these

Text Solution

Verified by Experts

The correct Answer is:1,2,3

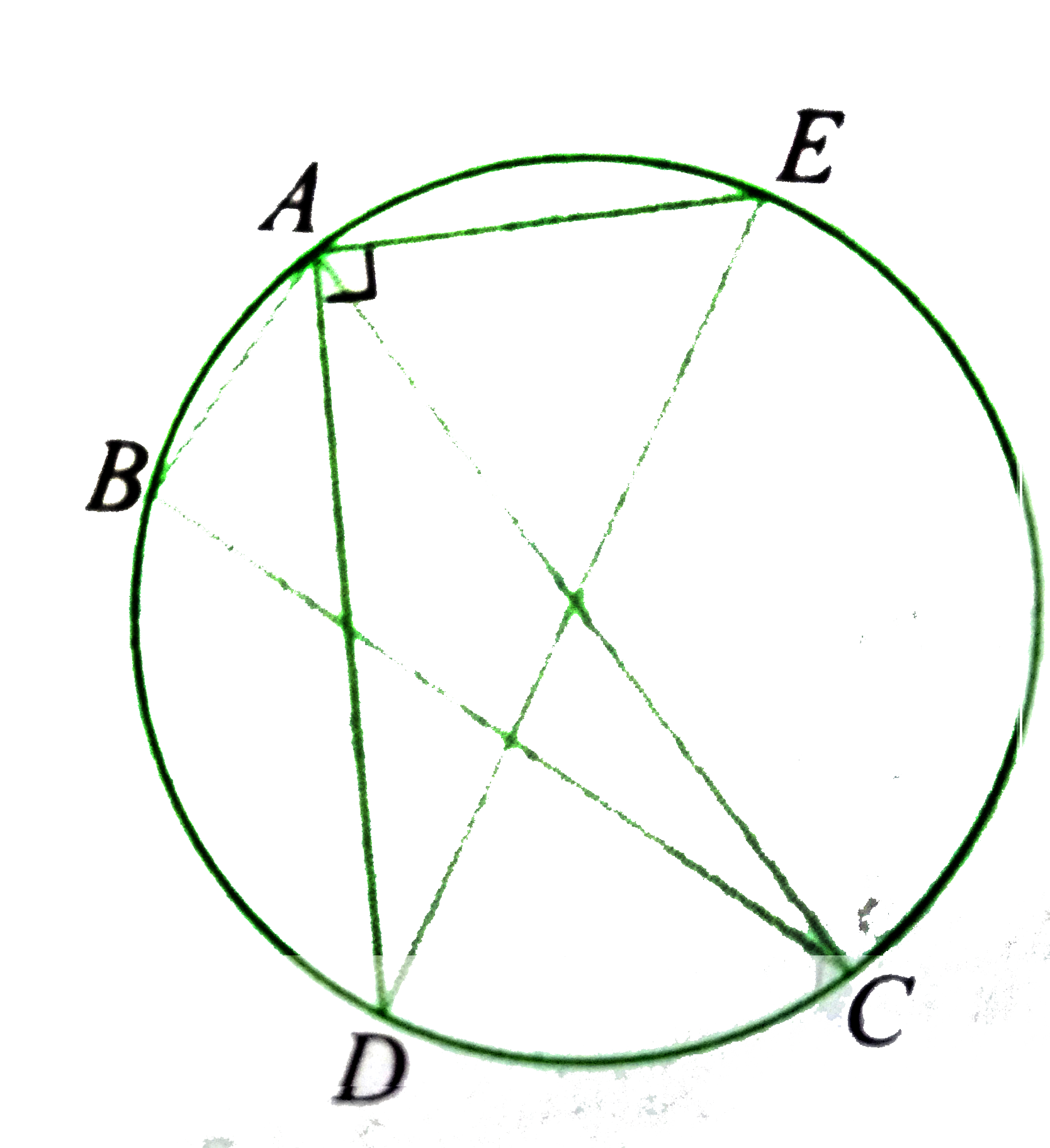
Orothocentre of $Δ A D E$ is A itself circumcentre is at origin. Hence, centroid is also a fixed point.

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
AD is the median of ABC and E is any point on AD. Which of the following statement is true ?

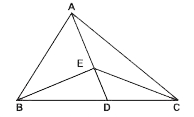Aar $(Δ A B D) > ar (Δ A C D)$
Bar $(Δ A B D) < ar (Δ A C D)$
Car $(Δ A B E) = ar (Δ C E D)$
Dar $(Δ A B E) = ar (Δ A C E)$
Question 2 - Select One
Area of the equilateral triangle inscribed in the circle $x^{2} + y^{2} - 7 x 9 y + 5 = 0$ is
A $\frac{155}{8} \sqrt{3} s q u n i t s$
B $\frac{165}{8} \sqrt{3} s q u n i t s$
C $\frac{175}{8} \sqrt{3} s q u n i t s$
D $\frac{185}{8} \sqrt{3} s q u n i t s$
Question 3 - Select One
In a triangle ABC, internal bisector of $∠ A B C$ and external bisector of $∠ A C B$ meet in D. Which one of the following is true ?
A $∠ B D C = ∠ B A C$
B $∠ B D C = \frac{1}{2} ∠ A B C$
C $∠ B D C = ∠ D B C$
DNone of these

CENGAGE-CIRCLE -Exercise (Multiple)

Home
Ask Doubt
Profile