Normal to the circle x2+y2=4 divides the circle having centre at (2,4) and radius 2 in the ares of ratio (π−2):(3π+2). Then the normal can be Solution in Tamil
y=x
y=3x
y=5x
y=7x
The correct Answer is:1,4
Normal to the circles x2+y2=4 passes through its centre (0,0)
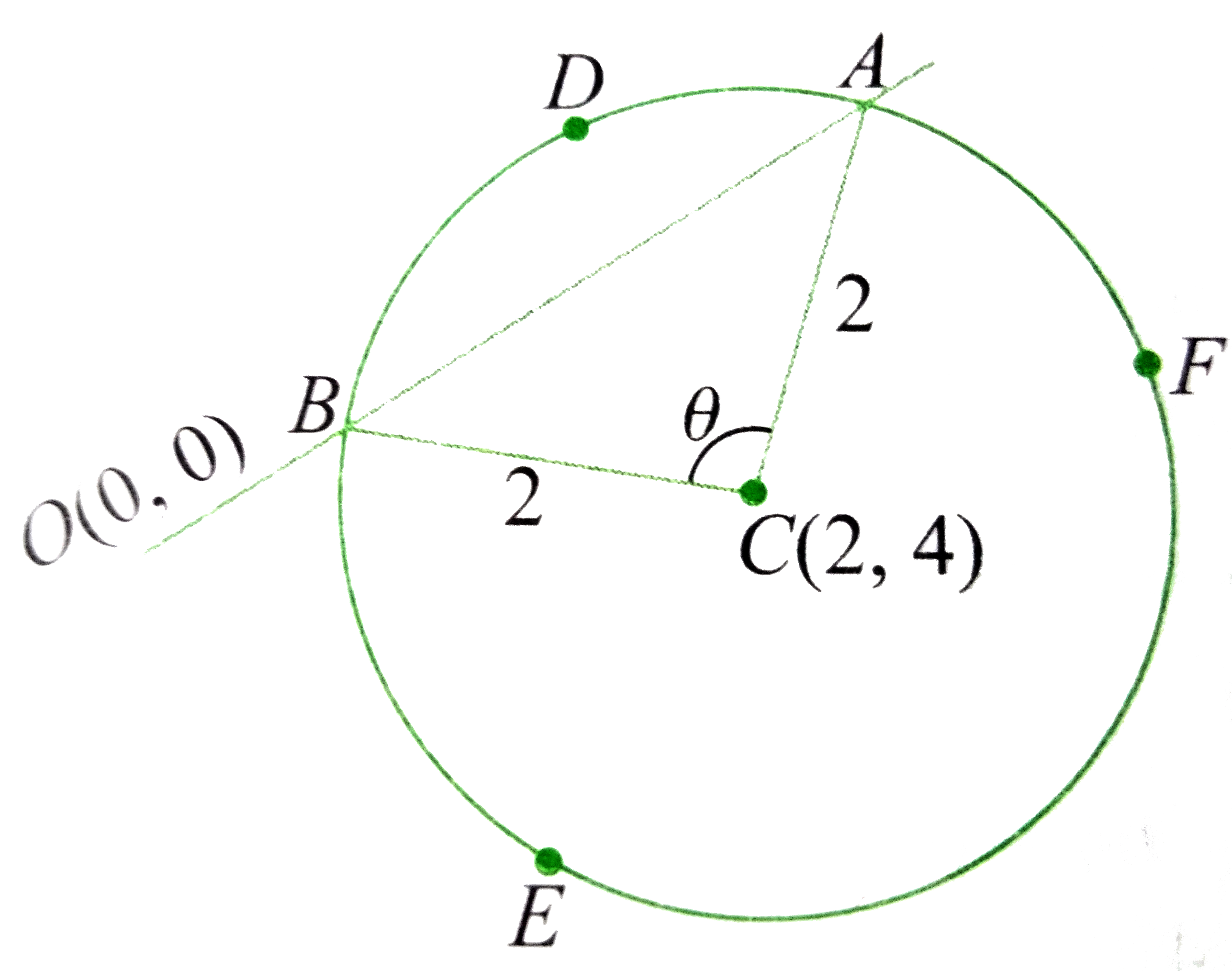
So, equation of normal is y=mx.
Now, according to the question.
Area of regio ADBAArea of regioN abefa=π−223π+2
∴[π(2)22π.θ−12(2)2sinθ]π(2)2−[π(2)22π.θ−12(2)2sinθ]=π−23π+2
⇒θ=π2
∴Distance of centre of circle from line =2cos.π4
⇒|4−2m|√1+m2=√2
⇒m=1,7
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)46videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)1videos
CIRCLE
- BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Single)109videos
CIRCLE
- BOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
Similar Questions
Each side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
03:39View SolutionLet C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point
03:06View SolutionThe number of rational point(s) [a point (a, b) is called rational, if aandb both are rational numbers] on the circumference of a circle having center (π,e) is a)at most one b) at least two c)exactly two d) infinite
03:05View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is05:37View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
00:43View SolutionIf the line ax+by=2 is a normal to the circle x2+y2−4x−4y=0 and a tangent to the circle x2+y2=1 , then aandbare
05:24View SolutionA circle with centre at (2,4) is such that the line x+y+2=0 cuts a chord of length 6. The radius of the circle is
01:09View SolutionThe radius of circle touching parabola y^(2)=x at (1,1) and having directrix of y^(2)=x as its normal is
02:21View SolutionNormal to the circle x2+y2=4 divides the circle having centre at (2,4) and radius 2 in the ares of ratio (π−2):(3π+2). Then the normal can be
02:47View SolutionThe centre and radius of the circle (x+2)2+(y+4)2=9 are
02:22View SolutionFind the equation of tangent and normal at
(3,2) of the circle x2+y2−x−3y−4=0.04:57View Solution" Equation of normal at "'theta'" to the circle "^(x^(2)+y^(2))=r^(2)" is "
07:22View SolutionThe normal at P(2,4)to y2=8x meets the parabola at Q. Then the radius of the circle on normal chord PQ as diameter is.
07:36View SolutionThe normal at θ of the circle x2+y2=a2 is
04:02View SolutionEquation of Normal at 'θ' to the circle x2+y2=r2 is
03:35View SolutionThe normal at θ of the circle x2+y2=a2 is
02:28View Solution

