The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3)

A

$\frac{10}{3}$

B

$\frac{3}{5}$

C

$\frac{6}{5}$

D

$\frac{5}{3}$

Text Solution

Verified by Experts

The correct Answer is:A

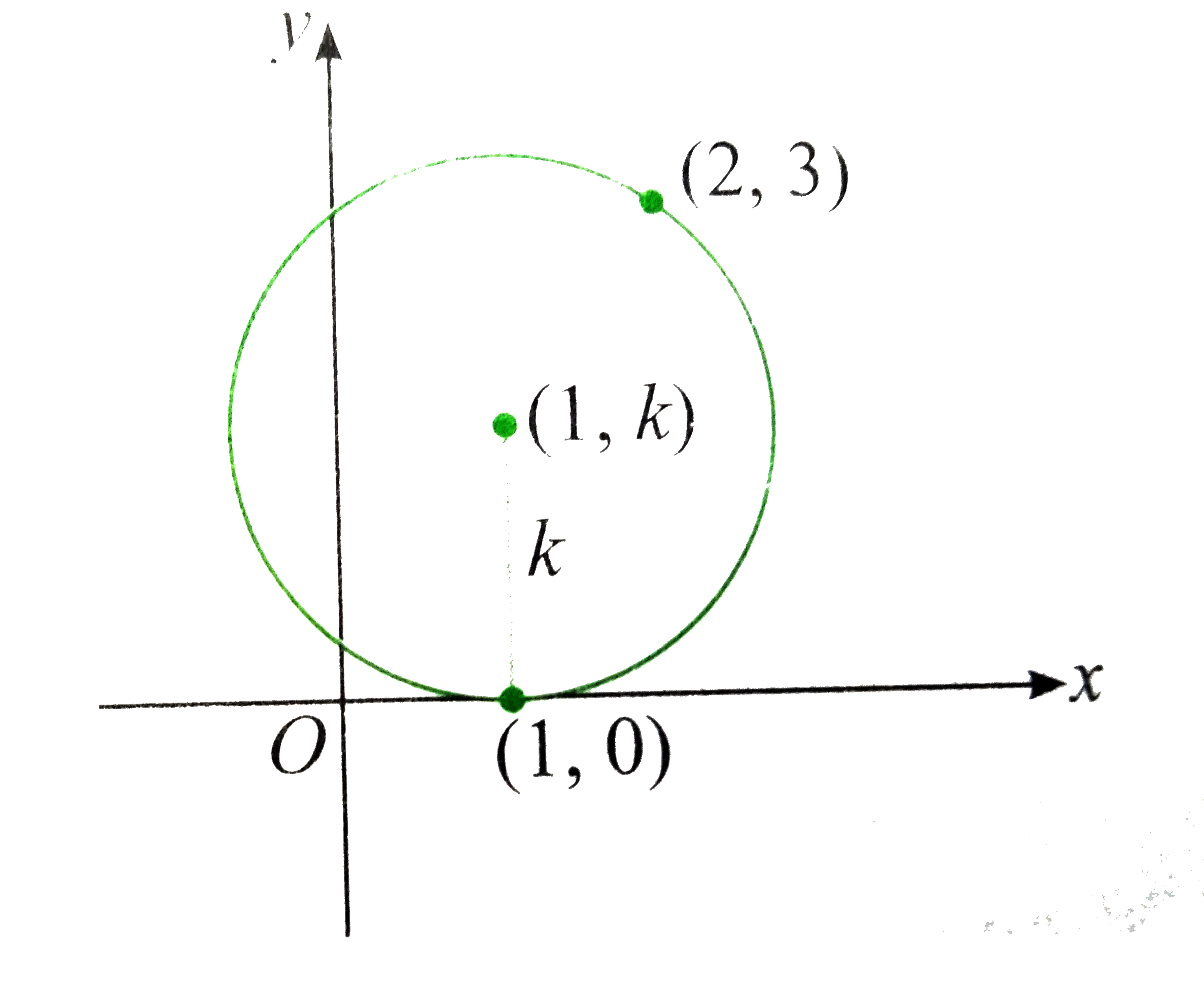
Circle touches x-axis at (1,0).
So, center of circle is $(1, k)$ and radius is k.
Hence , equation of circle is $:$
${(x - 1)}^{2} + {(y - k)}^{2} = k^{2}$
It passes through the point (2,3), so
${(2 - 1)}^{2} + {(3 - k)}^{2} = k^{2}$
$∴ 1 + 9 - 6 k + k^{2} = k^{2}$
$∴ k = 5 / 3$
$∴$ diameter $= 2 k = 10 / 3$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The length of the radius of the circle which touches the x - axis at the point (1, 0) and passes through the point (2, 3) is
A $\frac{10}{3} units$
B $\frac{3}{5} units$
C $\frac{6}{5} units$
D $\frac{5}{3} units$
Question 2 - Select One
The length of the diameter of the circle which passes through the point (2,3) and touches the x-axis at the point (1,0) is
A $\frac{5}{3}$
B $\frac{6}{5}$
C $\frac{10}{3}$
D $\frac{3}{5}$

CENGAGE-CIRCLE -JEE Main Previous Year

Home
Ask Doubt
Profile