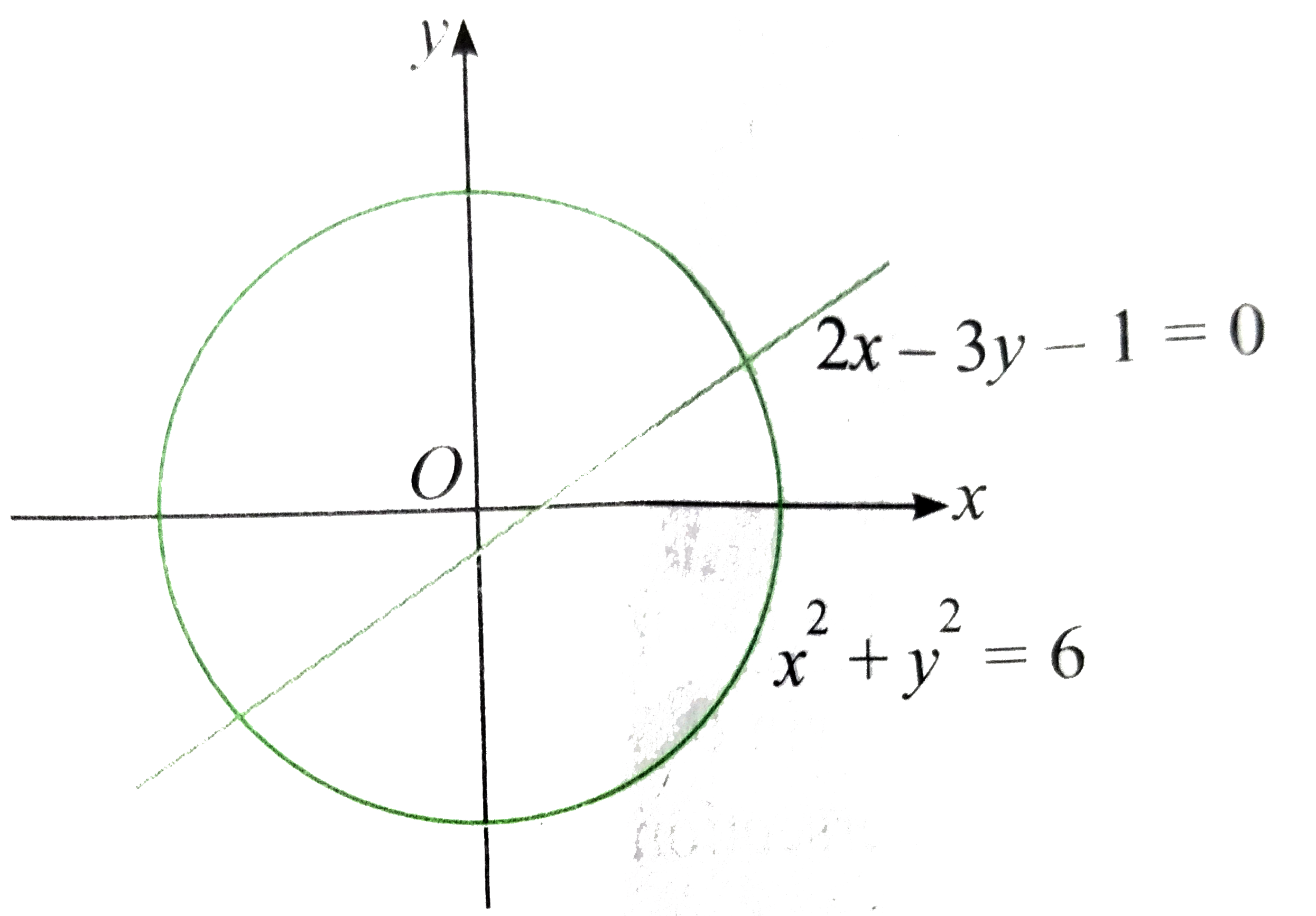
The straight line 2x-3y = 1 divides the circular region x2+y2≤6 into two parts. If S = { (2,34),(52,34),(14,−14),(18,14)}, then the number of point(s) in S lying inside the smaller part is
The correct Answer is:2
L=2x−3y−1=0
S:x2+x2−6=0
If L1>0 and S1<0 , then the point lies in the smaller part. Therefore, (2,3/4) and (1/4,−1/4) lie inside.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Main Previous Year
10 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
The straight line 2x-3y = 1 divides the circular region x2+y2≤6 into two parts. If S = { (2,34),(52,34),(14,−14),(18,14)}, then the number of point(s) in S lying inside the smaller part is
View SolutionThe straight line 2x – 3y = 1 divides the circular region x2+y2≤6 into two parts. If
S={(2,34),(52,34),(14,−14),(18,14)}, then the number of point(s) in S lying inside the smaller part is
View Solution
Knowledge Check
Let the straight line x = b divide the area enclosed by y=(1−x)2,y=0 and x=0 into two parts R1(0≤x≤b) and R2(b≤x≤1) such that R1−R2=14. Then b equals
A34B12C13D14If the straight line x=b divide the area enclosed by y=(1−x)2,y=0 and x=0 into two parts R1(0≤x≤b) and R2(b≤x≤1) such that R1−R2=14. Then, b equals
A34B12C13D14The parabolas y2=4xandx2=4y divide the square region bounded by the lines x=4, y=4 and the coordinate axes. If S1,S2,S3 are the areas of these parts numbered from top to bottom, respectively, then
AS1:S2≡1:1BS2:S3≡1:2CS1:S3≡1:1DS1:(S1+S2)=1:2
The straight line 2x−3y=1 divides the circular region x2+y2≤6 into two parts
If S=⎡⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢⎣234523414−141814⎤⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥⎦
then the number of points lying inside the smaller part is
View SolutionLet the straight line x=b divide the area enclosed by y=(1−x)2,y=0 and x=0 into two parts R1(0≤x≤b) and R2(b≤x≤1) such that R1−R2=14. Then b equals (A) 34 (B) 12 (C) 13 (D) 14
View SolutionProve that the point (2,−1) and (1,1) are on the opposite sides of the straight line 3x+4y−6=0.
View SolutionThe parabolas y2=4xandx2=4y divide the square region bounded by the lines x=4,y=4 and the coordinate axes. If S1,S2,S3 are the areas of these parts numbered from top to bottom, respectively, then S1:S2≡1:1 (b) S2:S3≡1:2 S1:S3≡1:1 (d) S1:(S1+S2)=1:2
View SolutionThe parabolas y2=4xandx2=4y divide the square region bounded by the lines x=4, y=4 and the coordinate axes. If S1,S2,S3 are the areas of these parts numbered from top to bottom, respectively, then
View Solution
