If the normal at P(2,3√32) meets the major axis of ellipse x216+y29=1 at Q , and S and S' are the foci of the given ellipse, then find the ratio SQ:S′Q.Solution in Tamil
Equatio of ellipse P(2,3√32)
∴e2=1−916+716
⇒e=√74
Hence , foci are S(√7,0)andS(−√7)
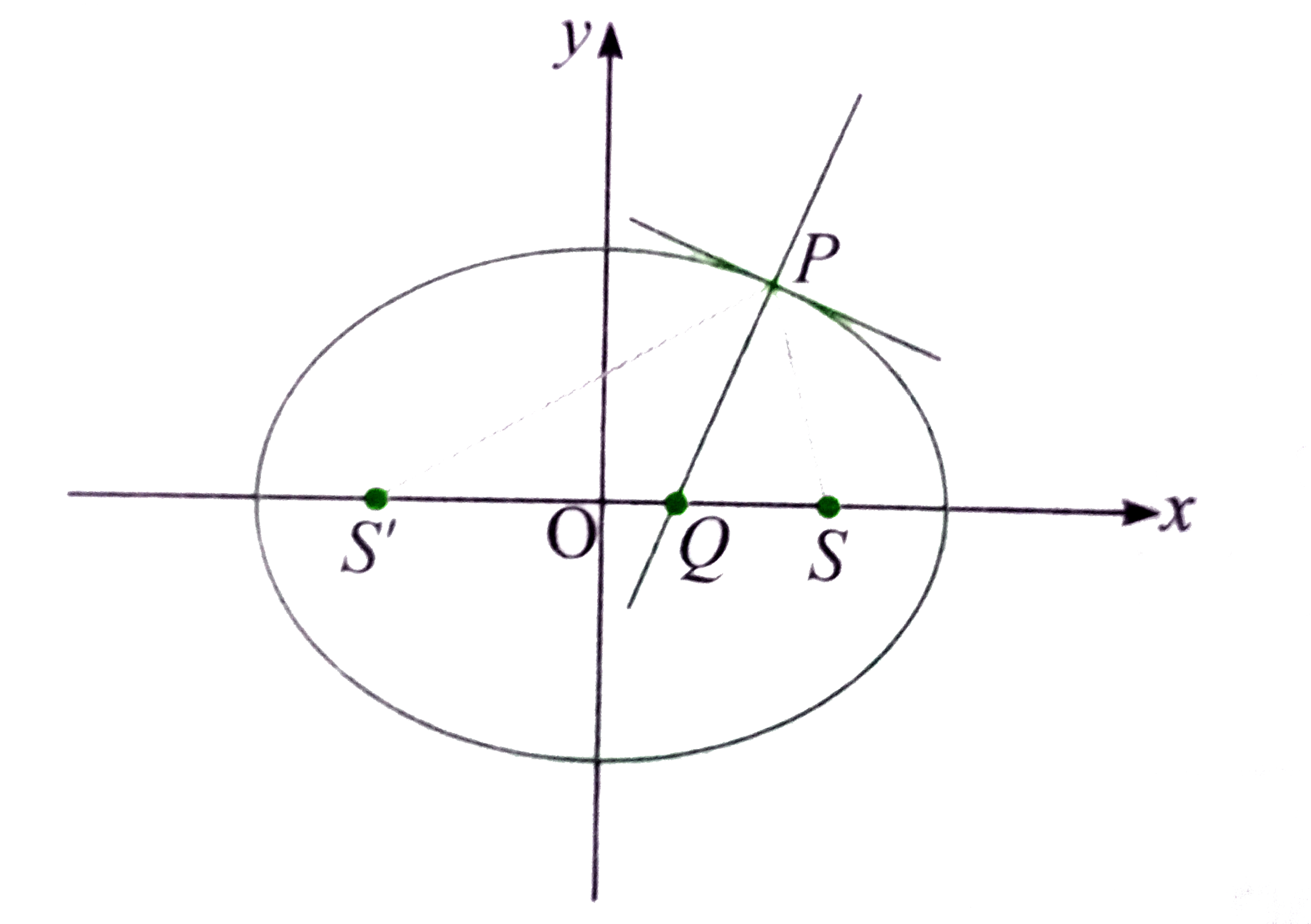
Normal at P bisects the angle ∠SPS''
Therefore, in triangle SPS' using bisector theorem, we get SQS'Q=SPS'P=a−exa+ex=4−√74×24+√74×2=8−√78−√7
Similar Questions
Column I, Column II An ellipse passing through the origin has its foci (3, 4) and (6,8). Then the length of its minor axis is, p. 8 If PQ is a focal chord of the ellipse x225+y216=1 which passes through S≡(3,0) and PS=2, then the length of chord PQ is, q. 10√2 If the line y=x+K touches the ellipse 9x2+16y2=144, then the difference of values of K is, r. 10 The sum of distances of a point on the ellipse x29+y216=1 from the foci is, s. 12
View SolutionIf SandS' are two foci of ellipse 16x2+25y2=400andPSQ is a focal chord such that SP=16, then find S′Q.
View SolutionIn the figure S and S∣ are foci of the ellipse,x225+y216=1 and P is a viable point on the ellipse.
Find the distance between S and S∣.
 .
.
View SolutionC is the centre of the ellipse x225+y216=1 and S is one of the foci. The ratio of CS to semi major axis is
View SolutionThe P is any point on the ellipse 4x2+16y2=64 whose foci are S and S′, then SP+S′P=
View SolutionLet S and S\' be the foci of the ellipse x^2/9 + y^2/4 = 1 and P and Q be points on the ellipse such that PS.PS\' is maximum and QS.QS \' is maximum. Statement 1 : PQ=4 . Statement 2 : If P is a point on an ellipse and S\' and S are its foci, then PS + PS\' is constant.
View SolutionIf SandS' are two foci of ellipse 16x2+25y2=400andPSQ is a focal chord such that SP=16, then find S′Q.
View SolutionColumn I, Column II An ellipse passing through the origin has its foci (3, 4) and (6,8). Then the length of its minor axis is, p. 8 If P Q is a focal chord of the ellipse (x^2)/(25)+(y^2)/(16)=1 which passes through S-=(3,0) and P S=2, then the length of chord P Q is, q. 10sqrt(2) If the line y=x+K touches the ellipse 9x^2+16 y^2=144 , then the difference of values of K is, r. 10 The sum of distances of a point on the ellipse (x^2)/9+(y^2)/(16)=1 from the foci is, s. 12
View Solution
