Tangents PQandPR are drawn at the extremities of the chord of the ellipse x216+y29=1 , which get bisected at point T(1,1). Then find the point of intersection of the tangents.Solution in Tamil
The correct Answer is:(14425,14425)
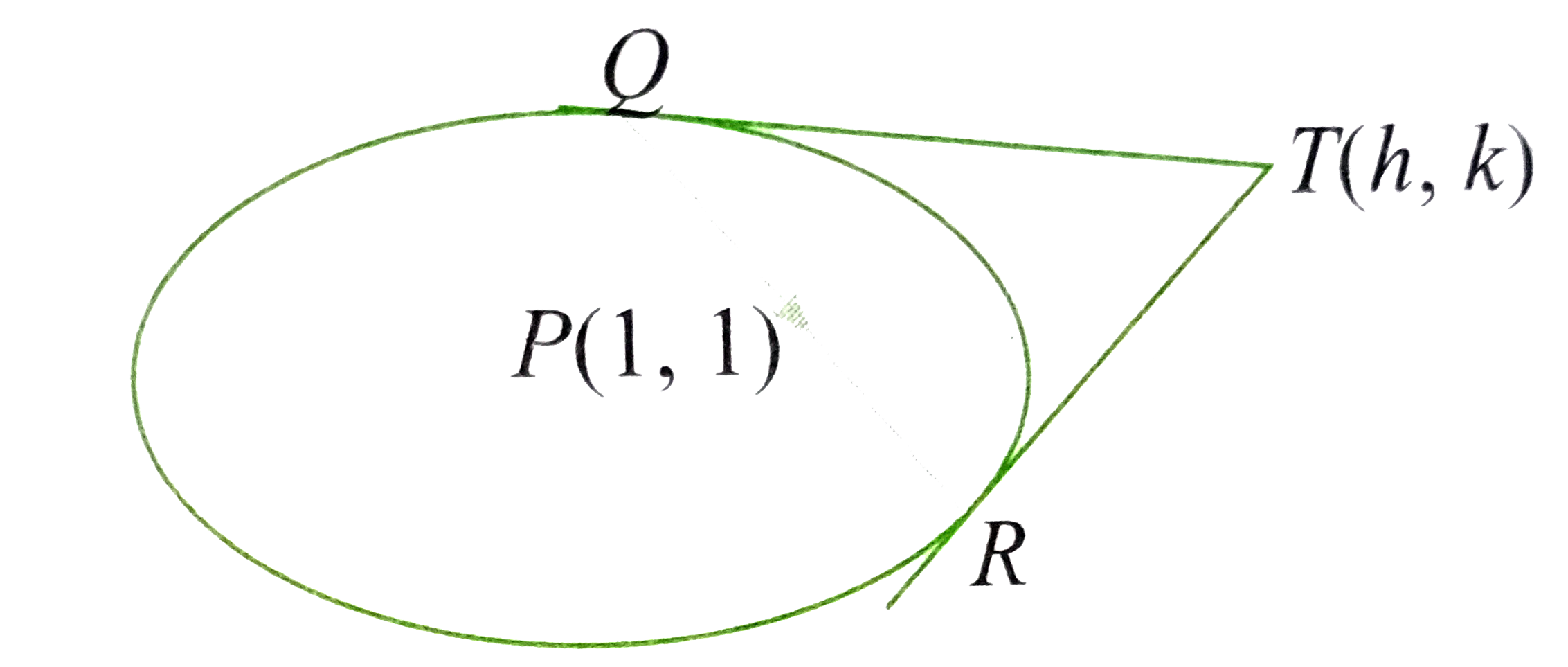
Eqution of chord having midpoint P(1,1) is
1⋅x16+1⋅y9−1=116+19−1
or x16+y9=25144
or9x+16y=25(1)
Also, line QR is chord of contact w.r.t. point (h,k).
It equations is
hx16+ky9=1
or 9hx+16ky=144 (2)
Equatiosn (1) and (2) represent the same stragith line.
∴9h9=16k16=14425
⇒(h,k)≡(14425,14425)
Similar Questions
Tangent are drawn from the point (3, 2) to the ellipse x2+4y2=9 . Find the equation to their chord of contact and the middle point of this chord of contact.
View SolutionIf from a point P, tangents PQandPR are drawn to the ellipse x22+y2=1 so that the equation of QR is x+3y=1, then find the coordinates of P.
View SolutionChords of the hyperbola x2a2−y2b2=1 are tangents to the circle drawn on the line joining the foci asdiameter. Find the locus of the point of intersection of tangents at the extremities of the chords.
View SolutionTangents P Qa n dP R are drawn at the extremities of the chord of the ellipse (x^2)/(16)+(y^2)/9=1 , which get bisected at point T(1,1)dot Then find the point of intersection of the tangents.
View SolutionIf from a point P, tangents PQandPR are drawn to the ellipse x22+y2=1 so that the equation of QR is x+3y=1, then find the coordinates of P.
View SolutionTangent are drawn from the point (3, 2) to the ellipse x2+4y2=9 . Find the equation to their chord of contact and the middle point of this chord of contact.
View SolutionTangents PQandPR are drawn at the extremities of the chord of the ellipse x216+y29=1 , which get bisected at point T(1,1). Then find the point of intersection of the tangents.
View Solution
