The coordinates (2, 3) and (1, 5) are the foci of an ellipse which passes through the origin. Then the equation of the (a)tangent at the origin is $(3 \sqrt{2} - 5) x + (1 - 2 \sqrt{2}) y = 0$ (b)tangent at the origin is $(3 \sqrt{2} + 5) x + (1 + 2 \sqrt{2} y) = 0$ (c)tangent at the origin is $(3 \sqrt{2} + 5) x - (2 \sqrt{2} + 1)) y = 0$ (d)tangent at the origin is $(3 \sqrt{2} - 5) x - y (1 - 2 \sqrt{2}) = 0$ Solution in Tamil

tangent at the origin is $(3 \sqrt{2} - 5) x + (1 - 2 \sqrt{2}) y = 0$

tangent at the origin is $(3 \sqrt{2} - 5) x + (1 + 2 \sqrt{2}) y = 0$

tangent at the origin is $(3 \sqrt{2} - 5) x - (2 \sqrt{2} + 1) y = 0$

tangent at the origin is $(3 \sqrt{2} - 5) - y - (1 - 2 \sqrt{2}) = 0$

Video Solution

Text Solution

Verified by Experts

Tangent and normal are bisector of $∠ S P S$
Now, the eqaution of SP is $y = 3 x / 2$ and that of SP is y=5,
Then equation of angle bisectors are
$\frac{3 x - 2 y}{\sqrt{13}} = \pm \frac{5 x - y}{\sqrt{26}}$
or $3 x - 2 y = + \frac{5 x - y}{\sqrt{2}}$
Therefore ,the lines are
$(3 \sqrt{2} - 5) x + (1 - 2 \sqrt{2}) y = 0$
and $(3 \sqrt{2} + 5) x - 2 \sqrt{2} + 1) y = 0$
Now, (2,3) and (1,5) line on the same side of $(3 \sqrt{3} - 5) x + (1 - 2 \sqrt{2} y = 0$ , which is the equation of tangent.

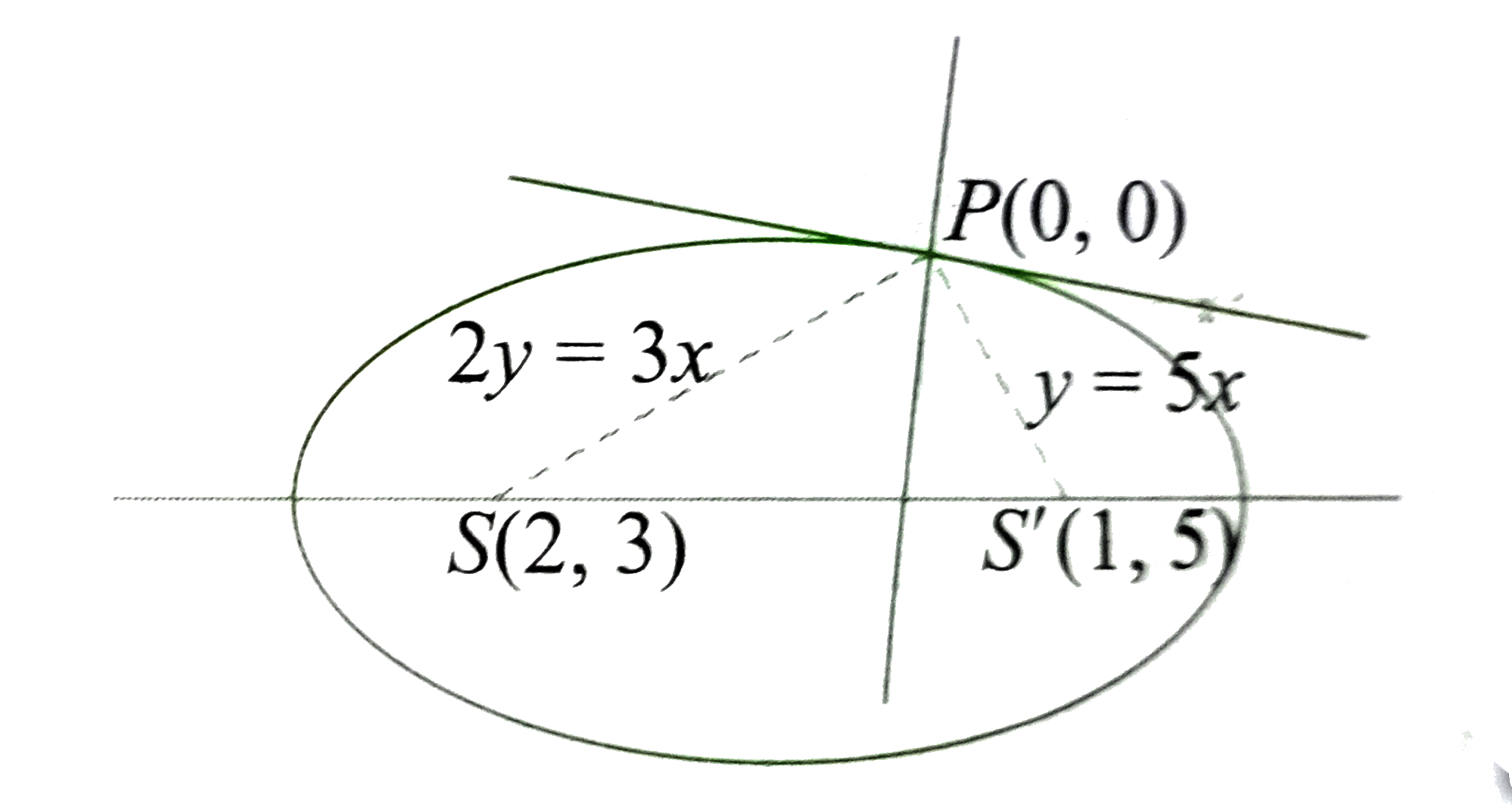
Points (2,3) adn (1,5) a line on the different sides of $(3 \sqrt{2} + 5) x + (2 - \sqrt{2} + 1) y = 0$ , which is the equation of normal

Updated on:21/07/2023